Two-dimensional crystals can grow on a surface within minutes. What they will look like depends on the solute and its concentration, the solvent, the temperature, the humidity, and many other factors. The result is often a surprise.
1. The Experimental Procedure
1.1. General Remarks
One differentiates between two forms of 2D crystals: In one form, they are as thin as atoms, for example, in graphene, consisting of carbon, or in stanene, made of tin. The other 2D crystals have a thickness of around 20 µm and are considered here. For their preparation and examination, one can spread a drop (50 µL) of a chemical solution on a microscope slide. After the solution has dried, one looks at sections of roughly 1 mm x 1 mm with a microscope.
1.2. Substances
For the cases considered here, the solute concentrations in water were varied between 0.5 % and 50 %. In many cases, the concentrations have an enormous influence on the crystal shapes, as exemplified in Figures 1 and 2. Mixing the substances with polymers, e.g., gelatin, polyvinyl alcohol, acacia gum, agar-agar, tragacanth, or lysozyme, also yields surprising results, as shown for example in Figures 3–5.
.jpg) |
|
.jpg) |
|
Figure 1. Crystallized citric acid (48 %). |
|
Figure 2. Changed pattern upon reduction of the concentration of citric acid (12 %; compare with Fig. 1). |
 |
|
 |
|
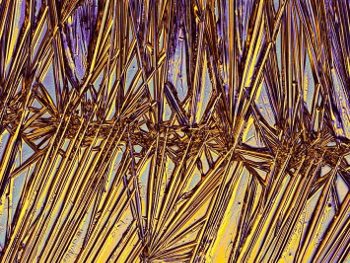
Figure 3. Formation of straight structures through addition of a polymer (lysozyme; 0,1 %) to copper(II) chloride (6 %). |
|
Figure 4. Straight structures through addition of a polymer (gelatin; 0.8 %) to ammonium chloride (6 %). |
 |
|
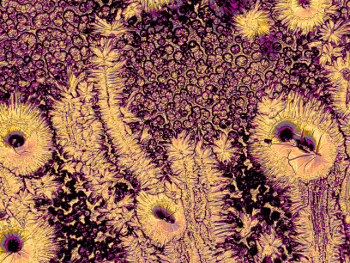
Figure 5. The addition of acacia gum (here, 0.8 % to 3 % threonine) does not form straight structures, as for other polymers, e.g., in Figures 3 and 4. |
Furthermore, the addition of sugars or sugar alcohols gives interesting results. While sufficiently high amounts inhibit crystallization completely, small concentrations cause a rounding of the crystals, as shown with trehalose in Figure 6. Both the inhibition and the crystal rounding with these substances account for the prevention of “razor-sharp” crystals, which may cut the cell membranes in temporarily dried or frozen animals [1].
 |
|
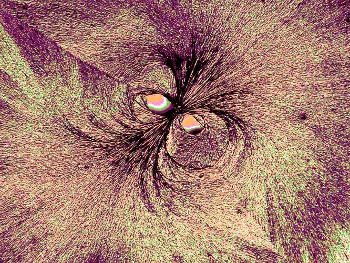
Figure 6. Needle-shaped crystals (copper(II) chloride; 6 %) are here bent by sugars (trehalose; 4 %). |
1.3. Spreading the Solutions on the Glass
The glass of the microscope slide is often not sufficiently hydrophilic so that the drop forms a “pearl”. This effect is stronger for certain substances, such as magnesium sulfate or caffeine. Depending on the supplier, some microscope slides are hydrophilic on first use, but lose this property by washing or rubbing. If necessary, one can coat the slide with an anti-fogging spray, such as those used for glasses or windshields, followed by gently dabbing off the product. The problem of “pearl” formation does not occur when using suitable solvents, such as ethanol, which leads to different crystals (see Figs. 7 and 8). Alternatively, one may add around 0.2 ‰ of a common dishwashing liquid.
 |
|
 |
|
Figure 7. Crystals of ascorbic acid from an aqueous solution (3 %). |
|
Figure 8. Like Figure 7, but from a solution in ethanol (3 %). |
1.4. Desiccation
In general, a drop spread over the glass takes about 20 minutes to dry and form crystals. However, some solutions, e.g., those of citric acid, proline, or β-alanine, attract water if the environment is too humid and, therefore, dry very slowly or not at all. Sometimes it helps to place some grains of the substance on the border of the solution layer to act as crystallization seeds.
1.5. Observations with the Microscope
After drying, one sees different structures under the microscope. One reason for this is that the structures depend on the layer’s thickness, which increases from the edge to the center. In addition, unnoticed dust or dirt can affect crystal growth. In any case, it is exciting to search for interesting crystals by slowly and vigilantly moving the slide under the microscope.
The crystallization also depends on the temperature and the humidity. One can record the values using a thermometer and a hygrometer on different days to determine their influence. The pictures in this article were taken at about 20 °C and humidities between 40 % and 70 %. To keep these conditions constant, a climate chamber with a hygrostat and a thermostat would be necessary.
The pictures are usually in black and white. If one wants to turn gray values into colors for better visualization, as was done in the present article, one can use image manipulation software which is freely available on the internet, for example, GIMP (GNU Image Manipulation Program).
2. What Can Two-Dimensional Crystals Teach Us?
2.1 Crystalline Order versus Chaotic Thermal Motion
On a wool thread hanging in a saturated solution, 3D crystals with symmetrical shapes, such as cubes, octahedra, etc. are formed within a few days or weeks. Such crystals are formed like brick buildings, the molecules of the solution gradually being bound at the most stable locations. Binding at other sites is also possible but does not last long due to the thermal motion, that is, the molecules break away from the crystal and migrate until they reach a more stable site. Such a process was described in detail and independently in the theoretical works of Walther Kossel and Iwan Stranski [2, 3].
In the experiments described here, the solution layer is so thin that the solvent usually evaporates within a few minutes and thus large numbers of weakly or non-bound molecules do not have time to reach the most stable binding sites. Only a fraction of the molecules, therefore, forms ordered structures, while the rest is subject to chance due to thermal motion. Thus, the pictures in this report show a mixture of order and chaos. Because of the latter, no crystal looks completely like another, even if the ambient conditions are the same.
Figure 9 shows the presence of crystalline order particularly clearly by the repeated occurrence of a characteristic angle, as well as the occurrence of chaos in the smaller, unequal “branches”. All in all, a so-called fractal structure is observed in this figure, i.e., small image parts resemble larger parts, as in a tree.
 |
|
Figure 9. Crystals of silver nitrate (5 %) with ordered, characteristic angles and chaotic branches with fractal structure. |
2.2. Analogy to Frost Flowers
On windows with bad heat isolation and on car windows, ice crystals often appear in winter. They are explained as follows. The air is cold in the immediate vicinity of the window and the air around it is humid. The water vapor deposits itself as ice on the window and behaves analogously to the solute in this report. If the ice formation had enough time, only the characteristic hexagonal shapes would form, but the chaos of the water molecules in the air become frozen in the form of differently shaped “flowers”. Although the crystals in this report are caused by desiccation and the ice crystals by freezing, analogous physical processes take place in both systems.
2.3. Chaos Theory
Above, the word “chaos” was used in the sense of disorder. In the 1960s, the word “chaos” became used to describe an important feature of disorder, that of unpredictability. This feature has far-reaching consequences, e.g., in weather forecasting or cardiac arrhythmias.
The reason for unpredictability is a phenomenon in which small causes can have very large effects, which is also called the butterfly effect: “The flapping of the wings of a butterfly in India can trigger a storm in America months later”. To illustrate this statement, one can consider billiard balls. If one hits ball B with ball A and ball C with ball B, one can predict the course of ball C as an experienced player. But with only five balls hit consecutively, very small and uncontrollable muscle twitches play a large role. For 17 balls, the gravitational force of an observer is involved in the course of the last ball. With 49 balls, one would have to consider the gravitation of the entire Milky Way for a prediction [4].
With 2D crystals, one can easily verify the “butterfly effect“ by adding minute amounts of a foreign substance to the solution. This can have drastic consequences, as shown in Figure 10, as compared to Figure 1, or in Figure 11, as compared to Figure 7. Figure 12 also shows this effect. Note that in these cases the “butterfly” is not in a particular place, but tiny and everywhere, as in the case of gravity in the above example with the billiard balls.
 |
|
 |
|
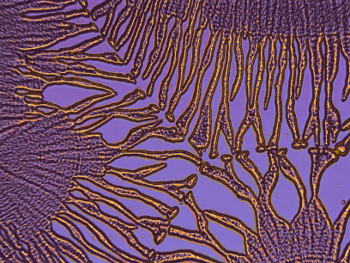
Figure 10. A very small addition of taurine (1 %) to citric acid (48 %, same as in Fig. 1) causes drastic changes (“butterfly effect”). |
|
Figure 11. A minute addition of ammonium chloride (0.015 %) to ascorbic acid (3 %, same as in Fig. 7) causes large changes. |
 |
|
Figure 12. A small addition of glycine (0.1 %) to copper(II) sulfate (10 %) causes unexpected changes. |
2.4. Diagnosis of Diseases and Species Identification
It has been claimed that by adding blood serum, urine, tears, or other body fluids, illnesses can be diagnosed via 2D crystals [5–8]. Other reports have claimed that the species of plants [9] or animals [10] can be determined by the addition of their juices or bodily fluids. However, changes in the ambient temperature or humidity can have a greater impact on the shape of 2D crystals than the addition of bodily fluids [11]. In addition, the thickness of the layer on the glass has an enormous impact. Keeping all influencing parameters constant is so complex that the mentioned method for diagnosis or species identification could not succeed. However, it was an irony of fate that ambitions in the field of medical diagnosis moved the author of this report to work in this field.
3. Additional Information
More details are given in a book [12] and in a publication for teachers [13]. In addition, there is an exhibition of 50 crystal pictures on the ground floor of the University Library in Dortmund, Germany, until June 26, 2018.
References
[1] M. Markus, Unsere Welt ohne Insekten? (in German), Franckh-Kosmos, Stuttgart, 2014, 180–181. ISBN: 978-3440143360
[2] W. Kossel, Über Krystallwachstum (in German), Naturwissenschaften 1930, 18, 901–910. https://doi.org/10.1007/BF01497028
[3] I. N. Stranski, Beitrag zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander und zur Frage der Bildung von Grimmschen Mischkristallen (in German), Z. Phys. Chem. A 1929, 142, 453–466. https://doi.org/10.1515/zpch-1931-s124
[4] M. Markus, Die Kunst der Mathematik (in German), Verlag Zweitausendeins, Frankfurt, 2009, 27–28. ISBN: 978-3861507673
[5] F. Lehmann-Grube, Über die Beeinflussbarkeit der Kupferchlorid-Kristallisation durch Liquor cerebrospinalis bei Meningitis tuberculosa (in German), Arch. Psychiatr. Z. Neurol. 1954, 182, 207–219.
[6] A. Selawry, O. Selawry, Die Kupferchlorid-Kristallisation (in German), Gustav-Fischer, Stuttgart ,1957.
[7] A. Solé, Stagoskopie (in German), Franz Deuticke, Wien, 1960.
[8] J. Murube, Tear crystallisation test: Two centuries of history, Ocul. Surf. 2004, 2, 7–9. https://doi.org/10.1016/S1542-0124(12)70019-8
[9] E. Pfeiffer, Kristalle (in German), Orient-Occident-Verlag, Stuttgart, 1930.
[10] A. Solé, Vergleichende Stagoskopie des Blutserums (in German), Österr. Zool. Z. 1955, 5, 366–376.
[11] J. Fasel, Einfluss von Polysacchariden und Proteinen auf anorganische Kristallisation (in German), Diplomarbeit, Technical University of Dortmund, Germany, 2009.
[12] M. Markus, Bildkraft der Substanzen: 2D-Kristalle zum Selbermachen (in German), Arnshaugk, Neustadt an der Orla, 2017. ISBN: 978-3944064772
[13] M. Markus, Zweidimensionale Kristalle (in German), MNU Journal 2018, 71 (3), 195–201.
The Author

Mario Markus, Emeritus Professor of Physics at the University of Dortmund, Germany, was Group Leader at the Max Planck Institute for Molecular Physiology, Dortmund, for a long time. Contact details and CV can be found at www.mariomarkus.com.
Also of Interest
- Poetry and Chemistry,
Vera Köster, Mario Markus,
ChemistryViews 2013.
https://doi.org/10.1002/chemv.201300010
Professor Mario Markus, scientist, artist, author, and poet, talks about what science can offer to art and how art can benefit science - Poems by Mario Markus based on the natural properties of the elements of the periodic table
- Digital Photography in Chemistry,
ChemistryViews 2014.
Low-budget solutions for imaging objects from chemistry using compact digital cameras with a microscope or a flatbed scanner




