Discussion Spawned Development in the Field
A recent Research Highlight on ChemistryViews.org on the nature of the Periodic Table of the Elements attracted a lot of readers and has stimulated an ongoing debate among those arguing as to whether or not there is a definitive format for this iconic tool. Intriguingly, however, the article and ensuing discussion has also spawned a development in this field courtesy of UCLA chemistry professor Eric Scerri.
“One of the most positive outcomes of the very popular ‘Periodic Debate‘ discussion has been that the relative virtues of the so-called ‘Stowe’ and the ‘left-step’ periodic table, in various formats, have been vigorously discussed,” Scerri says. “In the course of this debate I have come up with a compromise table which includes the best features of both types of systems.”
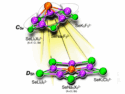
Stowe Table
The Stowe table is named for Tim Stowe who published his system on a website several years ago but has, apparently, published nothing since. Chemists have attempted to track him down, but he seems to have vanished from the community without a trace, leaving behind an interesting periodic legacy. “Many people interested in the periodic table have tried to track him down,” says Scerri, “but nobody has yet succeeded.”
Stowe’s system is four dimensional in the following sense: the x and y axes depict values of the m and s quantum numbers. In the case of the s or spin quantum number values are either positive or negative, while the values of the m quantum number can range from -l, through 0 up to +l in integer steps. The z-axis is taken as the n or main quantum number representing the main shell. The fourth dimension, which obviously cannot be depicted spatially, is shown by the use of different colors each of which denotes a different value of the l quantum number. In this way, the Stowe table seeks to depict the four quantum numbers of the electron that differentiates each atom from the previous one in the sequence of increasing atomic numbers.
However, the Stowe representation has several drawbacks, which is where Scerri’s new approach comes to the fore. The left-step table has received a great deal of attention in recent years. It was originally designed by the French engineer and polymath Charles Janet in the 1920s. However, with the advent of quantum mechanics and the quantum mechanical account of the periodic system it was realized that his system displays the elements in order of increasing n + l values of the differentiating electron. Many authors have claimed that this is a more natural system since electron filling accords with this criterion rather than increasing values of n.
New Modifications by Scerri
Scerri has now modified the left-step table by combining it with Stowe’s idea of using the quantum numbers explicitly to represent the elements in the periodic system. “The notion that n + l is more fundamental than n alone is key,” says Scerri. “The format I have now constructed depicts the arrangement of the elements in this fashion for elements 1 to 65 inclusive and can be easily extended up to 118 the currently heaviest atom and indeed beyond to elements that will in all probability be synthesized soon.” In what he now calls the Stowe-Janet-Scerri periodic system each level represents a particular value of n + l which take the form of horizontal periods in the case of the original Janet table.
Following Scerri’s introduction of this new layout in the comments of the ChemistryViews item, commenter Valery Tsimmerman, pointed out that Scerri’s efforts in re-working the Stowe table is bringing us closer to the realization of the numerical and geometrical regularities of the Periodic System. Tsimmerman also claims to have devised the perfect Periodic Table based on the concept of tetrahedral sphere packing.
Tsimmerman’s Concept of Tetrahedral Sphere Packing
Tsimmerman points out that chemists such as Henry Bent mentioned that every other alkaline earth atomic number equals to four times the pyramidal number, while Wolfgang Pauli noticed that length of periods are double square numbers: 2x(1, 4, 9, 16). This latter point is, Tsimmerman says, not surprising because square numbers are the sums of odd numbers 1, 1+3, 1+3+5, 1+3+5+7 … We know the meaning of odd numbers in the periodic system. They are the lengths of s, p, d and f blocks. Adding the number of elements in block rows results in the lengths of the periods. Adding square numbers results in pyramidal numbers: 1, 1+4=5, 1+4+9=14, 1+4+9+16=30. Multiply them by four and you will get every other tetrahedral number 4, 20, 56, 120 … Those are the atomic numbers of Be, Ca, Ba and Ubn. “Great scientists like Pauli, Niels Bohr and others were marveling at numerical relationships found in periodic system,” says Tsimmerman. He suggests that Scerri’s latest periodic table is not quite the final version and suggests that any further reworking of Stowe’s table will take us closer to a definitive 3D table.
“I hope that this system will not be just another periodic table to add to the depository of tables that people dream up every so often but may represent a definitive step forward in the quest for improved periodic tables,” Scerri told us.
- Periodic Debate, David Bradley
Mendeleev’s Periodic Table is, for many, the symbol of chemistry but is the current layout the best one?
including discussion mentioned in article
- More Periodic Tables




Remember that tetrahedral numbers are themselves sums of all odd or all even squares, since 4x any square is also a square. This also means that the electronic period lengths are simultaneously double AND half squares. Thus 2 is 2×1 and 4/2, 8 is 2×4 and 16/2 and so on. The original mapping of every other alkaline earth number to every other tetrahedral number was my discovery- connection to the pyramidal numbers was Valery’s finding. I found that leftward movement by triangular number amounts from the alkaline earth positions (within periods only) landed on midpoint positions within idealized half orbital rows- Valery pointed out that these were positions where quantum number ml=0. Jess Tauber
This is all getting too Platonic for me. Juggling around with four small quantum numbers you are bound to get lots of regularities, but I think the irregularities are more interesting. As for Z triads, there are 46 elements in the Janet table that do no belong to any triad, so how can that be fundamental? Leave the definitive table for Plato’s Heaven!
I said 46 elements not in triads; that should read 54 – nearly half of 120!
The odd numbered periods do not produce in-column triads, but the even-numbered ones do. However, interestingly, the odd triads’ means are the half-filled orbital positions for 2p,3d,4f respectively. Perhaps this is not just a mathematical curiosity but has some hidden meaning or function. In any case this does go back to the fact that only every other tetrahedral number corresponds to an alkaline earth atomic number. Intermediate numbers differ by monotonically increasing amounts: Alkaline earth-tetrahedral numbers, 2-1=1; 12-10=2; 38-35=3; and 88-84=4…. Valery commented on this a long while ago on the T3 List (tech.groups.yahoo.com/group/tetrahedronT3). Jess Tauber
I just learned, while researching literature on tabletop nuclear reactions (see http://www.lenr-canr.org/acrobat/HoraHlowenergyna.pdf), that the nuclear double triangular/tetrahedral number relations (which feed into the (semi)magic numbers, had been noticed at least as far back as 1948, from one E. Bagge, Naturwissenschaften 35, 376. Has anyone ever seen this? Boy that wheel just keeps getting reinvented (how many times did the Janet table get rediscovered by the proud new owners?). Jess Tauber
Yes Philip you are correct. As I have often written, about half of all possible Z triads are valid. This follows from the fact that period lengths repeat and is no indictment on triads themselves. The idea is not to maximize triads period, otherwise I would arrange them in a linear sequence and would have even more of them. The idea is to combine the natural phenomenon of property repetition with an approach that will correct some of the irregularities in the medium-long form table. I proposed an analogy to the change from atomic weight ordering to atomic number ordering although I do not imply that Z triads are as fundamental as Z itself. Perhaps I should be more modest about the claim. I am using Z triads to correct small trouble areas in the periodic table. None of the other criteria are completely replaced. Eric
I think that significance of atomic number triads, or Z-triads, as Eric calls them, has yet to be completely realized. I do not agree with Eric’s position that maximization of number of triads will somehow address the problems of the periodic system. Maximization of number of Z-triads seems to work well for confirming placement of He next to Ne. However, I think that majority of chemists would argue that it does not work as well with placing H next F. Traditional periodic system is the testimony of that. I believe that instead of maximization we should look deeper for basic reasons of double periodicity and, therefore, triads. As Eric noted, the apparent reason for the triads is the fact the lengths of periods recur. Why, then, he attempts to brake this basic regularity by turning first two periods of Janet’s LST into one?___ Perhaps, instead of maximization we should look for optimization of number of triads. Take, for example, long form of traditional periodic system, which has first period that does not recur, as the early a version of LST promoted by Eric. It can be observed that first group members of all but two groups do not belong to triads. Out of 32 groups only 2 groups, 2nd and 18th, are exceptions to this rule. Those two groups are the odd balls. Eric’s proposition of maximization of triads would increase the number of such exclusions from the rule by another 2 groups. It sure looks like a move in wrong direction. Optimization calls for decrease in number of triads by placing He next to Be. Optimization calls for identical first two periods, just as in Janet’s LSPT. ____ Some time ago Jess made interesting observation that every other alkaline earth element, beginning with second element Be matches every other tetrahedral number and all remaining alkaline earths are exact arithmetic means of those numbers. Even Helium, if counted among the alkaline earths, fits this rule if atomic number zero, that Philip calls for in his Chemical Galaxy, is considered. I believe that Eric is correct when he talks about looking at the elements in terms of Z, but it is simplistic to look at triads without regard to the relationship of atomic numbers to the tetrahedral numbers. ____After Jess’ mentioned above discovery, I modified Pascal triangle by suppressing all even numbers and using zeros instead of even numbers in one of the two second diagonals (see images at yahoo T3 group). The result was that numbers in fourth diagonal of modified Pascal triangle corresponding to three dimensional space exactly match halves of Z numbers of EVERY alkaline earth element. This type of numerical regularity is much more interesting than triads. Triads are simply outcome of this regularity on a higher level. Therefore, I choose optimization over maximization of triads, since this has much more interesting math at the foundation and remarkably fits the structure, as well as behavior of the elements.
Eric: You say ‘1/2 of all possible triads’, but there are no other possible triads (unless you prolong the sequence to element 170 to get 32 more), And you say it ‘follows from the fact that period lengths repeat’, but this sounds like what I’ve said all along: that triads are the trivial consequence of the structure of the periodic system.
OK, call it trivial if you like but it implies that H is in the wrong place in the conventional table. It should be in the halogens. That’s the only difference my proposal makes, apart from confirming that group 3 should be Sc, Y, Lu, Lr. But a movement of H is as momentous as moving He to group 2 as in the left-step table.
Valery says “Maximization of number of Z-triads seems to work well for confirming placement of He next to Ne. However, I think that majority of chemists would argue that it does not work as well with placing H next F. Traditional periodic system is the testimony of that.” If we are to be guided by the traditional periodic system this would also argue against moving He to group 2 surely, as you seem to favor. If we are trying to find a better or optimal periodic table the argument that it might go against the traditional one is rather puzzling!
Valery writes, “Eric’s proposition of maximization of triads would increase the number of such exclusions from the rule by another 2 groups. It sure looks like a move in wrong direction.” Please explain how my table does that. Which are the 2 more groups that violate maximization of triads. I hope you are not confusing the new suggestion Janet-Stowe-Scerri with my previous H in halogens table. They are 2 separate and conflicting proposals as I tried to explain.
I was referring to H/F LST table, not to your new table, which is more consistent with my views regarding position of H and He. The two more groups that I referred to, that violate the optimization (not maximization) of triads are 1st and 17th. By that I mean that, if H is moved to halogens, first members of halogen and alkali groups will become parts of the triads, unlike groups 3 through 16, where first members are not members of triads. In Janet’s LSPT all 32 groups follow first member rule without exclusion.
I don’t see why it matters if first members are or are not members of perfect triads. Can you explain to us why a first member rule should be an additional criterion. Can you also explain what do you mean by first member rule? eric
The first member rule is based on observation of all groups of the periodic system. It suggests that LSPT format is the most regular, since all group first members in LSPT follow the rule. The first member rule is consistent with recurrence of the lengths of the periods._____ The existence of triads is based on the fact that the lengths of periods recur. It is simply inconsistent to deny recurrence of the first period in order to justify two extra triads and, at the same time, to base the explanation of triads on a basis of such recurrence of the rest of the periods.
Valery throws out the “first member rule” as though it were a well founded principle of science. We would need a far more detailed account of this “rule” The rule also makes it rather too easy to justify any placement whatsoever as far as first members are concerned. For example, somebody like Valery places He at the top of the alkaline earths and a chemist objects on the basis that the properties or lack of properties of He make this improbable. Valery can then reach for this first member rule to argue that any placement, however improbable, can be justified by claiming that the first member is completely anomalous. Perhaps Valery would be prepared to go through a few examples of just how anomalous first members actually are otherwise this will not impress chemists very much. Nor is it very convincing to claim that the periodic table is now completely out of the hands of chemists and that crude reductionism according to the number of outer electrons in an atom is all that matters.
Triads are a consequence of the structure of the system, and a consequence cannot determine a structure. The difference between H and either Li or F is very marked; by its strong preference for covalent bonding it resembles C more than any other element. Not quite as peculiar as He. The oddness arises surely because in the K shell there cannot be an octet of 2 s and 6 p electrons.
An interesting article on elements beyond 118 can be found at______ http://www.labnews.co.uk/laboratory_article.php/6691/2/Pointless-additions%27_________. This is relevant to the present debate because Martin Channon for example interprets the Stowe table to mean that there cannot possibly be any elements beyond 120, while Philip Stewart frequently dismissed the search for super-heavy elements.
I haven’t dismissed the search for super-massive elements; I just said the place to search is in the crust of neutron stars. I don’t see how we can pile on enough neutrons for stability under terrestrial condiditions.
Hi Philip._______Yes but Valery is claiming that this is a universal rule that applies to all 32 groups and has not given any arguments for it. He will presumably appeal to chemical behavior in order to do this while being prepared to ignore the obvious chemical similarity between He and the other noble gases.______. The first member rule is by no means generally accepted or clear. Henry Bent, its leading champion uses it to argue for He above Be while Bill Jensen who first discussed it in the literature uses it to argue against He above Be as I discuss in my book. _________________ I am not claiming that triads can determine the structure of the periodic system from first principles, just that they might be useful in making one small correction, namely the position of H. This is also far more acceptable on chemical grounds than placing He above Be !
Actually stellar phenomena may be TOO energetic to create super-massive nuclei, which is why we never actually see them. We might rather want to ‘sneak’ neutrons into these elements via low energy table-top experiments, atom by atom so we don’t blow ourselves up in the process, within metallic matrices where coulombic barriers are said to be overcome in unusual fashion, and compound nuclei formed. I’m still not convinced this is all real, and the unwillingness of these folks to share a conversation or two is troubling, but they HAVE been burned several times since the days of Pons and Fleischer. Do they deserve it? Time will tell. In the meantime perhaps the best place to look is in the cores of exploded metallic asteroids, where such processes might have occurred naturally. After all, who expected to discover ancient natural fission reactors from the days when the U235/U238 ratio was MUCH higher than it is today. Add good sized electric pulses and hydrogen and you’re in business. Did any floating metal ever face these conditions in the early solar system? Jess Tauber
Until the first-member ‘rule’ can be deduced from first principles it will remain an observation rather than a rule, but H and He are the elements for which oddness can be so deduced; it follows from the peculiarity of the K shell, which allows only one orbital, also the fact that removal of electrons leaves a naked proton..
I am okay with leaving first member “rule” as an observation for awhile. But it is hard to deny that structurally He is closer to Be than to Ne. The question is rather what Periodic system is supposed to classify. Is this classification of atoms or it is classification of their behavior? If it is classification of atoms, then He should be next to Be, as well as H next to Li. If this is classification of behavior, then Eric is right.____Reading Mendeleev’s words “…Properties, such as the optical and even the electrical or magnetic ones, cannot serve as basis for the system naturally, since one and the same body, according to the state in which it happens to be at the moment, may show enormous differences in this regard…” makes me believe that he would be in support of classification based on attributes of atoms, not on properties, had he known what we now know____ In that case there would be only one periodic table. Isn’t it what you are looking for?
Valery, “structurally” He is as much like Ne (full shell) as it is like Be. Why should number of electrons present take presence over number if electrons absent for a full shell? If what you say about atoms being more relevant than properties were correct then physicists would have accepted the left-step table long ago. They have not because they are too sensible to believe that chemistry is nothing but present day quantum physics. They give the last word on the periodic table to chemists and chemists will not place He in the alkaline earths for the time being at least. Of course we can indulge in science fiction and suppose that in 300 years time there will be chemical evidence for placing He above Be but is that really what this is about? eric eric
If Periodic Table layout had already been decided by the chemists and the physicists are in agreement with them, why do we even wasting our time discussing it? The Last, Definitive Periodic Table has been around since beginning of 1900’s. No point to discuss it further. Right?____ By the way, having full shells do not quite make He structurally similar to Ne. Those shells happen to be different and He, just like Be, do not have p-electrons which are abundant in Ne .____ Also, physicists do use Left Step PT and that is why it is called Spectroscopic Table.___ Talking about use of the Periodic Table, I have not heard that anybody has been using any other layouts, besides Mendeleev’s short form in some East European countries and very, very few people use ADOMAH Periodic Table to teach about electron configurations as well as to prepare home work. That is about it for now.
Chemistry is mainly limited to the behaviour of substances over a narrow rang of temperatures and pressures on a watery planet. Physics is far more general and has given us information that can be used to explain the properties that chemists are interested in, but surely it is that more general view that should take priority. Anyway, I don’t understand how Eric can be so stuck on the properties of He and at the same time be so enthusiastic about the Stowe table, which is very much a physicist’s representation, with H and He under Li and Be.
Philip let me explain again. I now have two conflicting proposals out there and I am not particularly “stuck” on either of them. One has He in the noble gases (Z-triads based) and the newer one has He in the alkaline earths (Janet-Stowe-Scerri system). So far I see no compelling argument for supporting one or the other more strongly, despite the title of this website, and I am using this forum in the hope of subjecting both proposals to as much criticism as possible. Is that OK or do I have to play the game of rigidly “sticking” to one proposal? Incidentally, has anyone heard from Henry Bent recently?
I know that Valery has Henry’s phone number, I have it somewhere as well. As for properties of chemicals it is interesting that even supposed dimensionless constants seem to vary in the universe of space and time- the fine structure constant changes in astronomical measurements depending on what direction one is looking at. And radioactive decay rates vary depending on whether the sun is flaring or how close the earth is to it, indicating effect of neutrino flux on nuclear stabilities. Things are FAR more interesting than we thought. Perhaps the particular chemical behaviors we unendingly argue about are just the local balance. Jess Tauber
Eric, if your other conflicting proposal is the one with H and the halogens on the left, and the O group on the right, I’m afraid for me it is a non-starter. It has a pretty symmetry, at the cost of putting the f block as an appendix, but it would be unhelpful and indeed confusing for people learning chemistry. It mixes shells and has gaps and breaks where none is justified. Nor do I see “Janet-Stowe-Scerri” as an advance on Janet or Adomah. I agree with Valery, there is nothing to discuss.
Well, I wish someone would answer my prior question about what counts as sphericality in nuclei. At least THAT should be relatively definitive . Jess Tauber
I have published two forms of the H in the halogens table. The one you mention and another one which has a more pleasing shape and does not show pseudo lateral symmetry. The paper appeared in the Journal of Chemical Education and I am sending you a copy via E-mail now. You have commented on it before and said that it was a form that Janet himself toyed with for a while. If shape matters so much, which it does not to me, then I give you that version of the H in the halogens table. Something you said about gaps, is resonating with me recently. It occurs to me that there is one similarity between my H in the halogens (both formats) and Janet’s LST and also Janet-Stowe-Scerri as compared with the traditional medium-long form. It is that all these alternative forms place H right next to He. Can we discuss whether this is an advantage or not perhaps since none of the usual partisanship should intrude? To what extent does the placement of H and He as widely separated in the medium-long form table represent a mistake or misrepresentation? Jess I think you are asking the wrong people.
Eric: the table in your 2008 article was Janet’s Version I in his article of May 1928, replaced by his definitive Version III in his article of November of that year. It is also the table published by L M Simmons in his article in J Chem Ed in December 1947. He knew of Janet’s work only from the disastrous article in Chemical News, and he rather ungallantly said: “[His] insistence on coiling the chart, together with the paucity of explanation, cause Janet’s table to be regarded as only touching the fringe of the present arrangement.” He too abandoned his copy of Janet Version I in in his article in J Chem Ed in December 1948 and opted for the full Janet table. So you are the only person who has not so far moved from Version I to Version III.
Nice to be unique in at least one respect! So what about the further point I raised? How relevant is it to close the gap between H and He in the opinion of the punters on this forum? Is it just cosmetic? Does it represent a real advance over the medium-long form table? eric
I believe that H and He belong next to each other, in that I agree with Eric. I also believe that H has to be above (or next) to Li, in that I agree with traditional periodic table. Finally, I believe that He belongs next to Be. In that I agree with Janet.___ Helium structurally resembles Be more than Ne. Eric’s argument that He is structurally close to Ne because both have completely filled shells is not valid, because having shells completely filled does not make elements structurally similar. For example, Zn and Yb also have shells completely filled, but it does make them similar neither to Ne, nor to He. This leaves only one Eric’s table that is more or less agrees with my views: Janet-Stowe-Scerri. It is certainly improvement to Stowe, because it is based on n+l. However it has few serious draw backs: 1) absence of tie lines makes it hard to follow elements from layer to layer, finding the elements without already knowing where to look for them is also hard; 2) electron shells are left unidentifiable; 3) color is used for marking subshells, therefore it can not be used to identify families/properties of the elements.
Helium has first shell completely filled, Ne has first two shells completely filled, Zn has first three shells completely filled and Yb has first four shells completely filled, but only He and Ne have all shells completely filled because both are light elements. No other noble gases have completely filled shells. If we accept that completely filled shells make He and Ne structurally similar, we can not say the same about Ne and Ar, since Ar does not have all shells filled.
All gaps and breaks in the uninterrupted sequence of elements are the artificial result of chopping it into sections. Only a spiral or helical representation avoids this.
Except that one kinked uninterrupted sequence, my Mendeleev’s Line model, folds neatly into a tetrahedron. It takes two mirror-image T3 models, bisects them at equivalent positions, and then recombines them so that each new model has one half from one, and the other from the other mirror-image model. It retains certain symmetries, for instance all the s-block elements flank an equatorial bisection. Because of difficulties I have in visualizing hidden elements (in this case both literally and figuratively), it is taking a long time to see if other features of the model conform to known anomalies in 2D tables. The line starts just offset from the center of the figure. Because filling within periods involves switchback folding of subperiods, and then period blocks fold in a different way (analogous to beta sheet versus alpha helix in protein structures), one cannot consider this model to be any kind of single helix or spiral stucture. Jess Tauber
Philip. Your point about all gaps being artificial is of course valid, but some gaps are more artificial than others. For example the gap between H and He in the conventional or medium-long form. One can ask the question about gaps within a 2-D representation in order to weigh up the pros and cons of the medium-long form and some of the other alternative 2-D forms that have been discussed here. Valery, your points about full shells of various kinds are interesting. I need to make a more systematic survey of full-shells of all kinds. Thanks for moving the discussion forward over this question.
Eric, when you do your survey of full-shells I suggest you to use ADOMAH PT. I think it is especially convenient for such purposes. You will find that elements He, Ne, Zn and Yb, that mark completion of 1st, 2nd, 3rd and 4th shells, are located in left bottom corners of s, p, d and f blocks respectively. Valery.
OK I will. Here is my revised point. Consider a short form table, by which I mean an eight column table which excludes both d and f block as footnotes. ________________________ Now He and Ne are similar and so are all the other noble gases in having full shells. So I mean full shell in the sense of full s and p orbitals. After all most of the noble gases do not have strictly full shells, only He and Ne in fact do. ____________________The fact remains that they are chemically very similar. So structurally, in the sense of having full s and p orbitals He and Ne ARE SIMILAR. Why is this similarity any less relevant in the sense of electronic configuration, than the similarity between both He and Be having as s2 configuration. And to turn your argument back onto you, so do most of the transition metal atoms have an s2 outer shell. _______________Surely you don’t propose placing He together with Be and most of the transition metals just because of an s2 outer shell? There is more to the periodic table than a purely reductive view. ______________The interest in the table and its lasting value lies in the fact that it crosses levels and remains relevant at multiple levels from the macroscopic to the microscopic and in between. Your highly reductive approach, apparently shared by Philip, is counter-productive in my view.
I discovered quite by accident today a new series of 3 one-hour episodes, on the Science Channel here in the eastern US, called ‘Unlocking the Universe’, which details the history of chemistry. Only into the first few minutes of it, but it looks quite good. These series tend to repeat on these cable channels, so you should be able to catch it either tonight or in the next days/weeks. Jess Tauber
Yes this is a repackaging of a series first shown on UK TV called Chemistry A volatile History. The quality is mostly very good. I was a consultant on the original series and am mentioned in the credits of one or two of the episodes directly connected with the periodic table and Bohr’s model of the atom. The narrator is the British-Iraqi physicist called Jim Al-Khalili. As a result the material is viewed a little too much from the physics point of view. You can also view the whole thing on youtube by searching for “Chemistry a Volatile History”. Also see, http://topdocumentaryfilms.com/chemistry-volatile-history/
I’m not a reductionist. Ecology is the most irreducible of the sciences. But the great progress of the 1860s was the move from classifying elements by their behaviour to classifying them by numerical values, RAM and valence. Once Z had replaced RAM and quantum numbers had been discovered, it became possible to represent the elements on that basis alone. The electronic structure explains much behaviour (not all; relativistic effects appear in heavy elements), but it is inconsistent to misrepresent the position of just two elements on the basis of behaviour. Valery’s table is unique in showing clearly both the completion of periods and the completion of shells. There remains the mystery of why Ar behaves like a noble gas with an incomplete M shell, when Kr and Xe can react with F. There is no mystery with He, since He++ would be a naked alpha particle.
He and Ne as structurally similar, as Zn and Yb are, not as Zn and Cd though._____If we were able to look at the atoms in detail, we would be able to recognize that structural similarity between He and Be is much stronger than that between He and Ne.
Can’t we just agree that ‘Janet-Stowe-Scerri’ is not definitive? We should note that it places H and He under Li and Be, so Eric, you seem to have come back to your 2007 view.
Yes I agree the Janet-Stowe-Scerri is not definitive. And yes in a sense I have returned to my 2007 position as presented in my The Periodic Table, Its Story and Its Significance (2007). But I now have two conflicting proposals on the table, excuse the pun. I am presenting the H in the halogens proposal my Very Short Introduction to the Periodic Table book which is due out soon. I received the proofs from the publisher just today. These discussions have helped enormously to sharpen my views and I will be making small changes to the concluding chapter on alternative tables as a result of our conversations. ______Incidentally, while looking for something on my computer I accidentally came across a very nice version of the Timothy Stowe table (one m not 2 here). It appeared in the well-known, in the US at least, calendar that was issued by the I2R company each year for many years. They have become something of a collectors item. That’s I squared R. The Stowe table is shown along with an explanation of what it’s about. Could this be the original source, in which case it is conceivable that somebody connected with these calendars might know the origin of the Stowe table. All the best, eric. I would be happy to send copies of this Stowe table via E-mail on request.
Many elements in periodic system have structural similarities, but some are stronger than others. To determine the strongest structural similarities we should look at the characteristics of outer electrons. Them most definitive of structural characteristics is electron orbital angular momentum. ______Angular momentum of both outer electrons of He and Be and other alkaline earths is zero with quantum number l=0. Angular momentum of outer electrons of Ne, Ar, Kr and other “not so inert” gases is not (l=1).
The two proposals are in fact Janet Version I a.k.a. Simmons 1947, and Stowe modified in the light of Janet Version III. I don’t think the latter will ever be much used, if only because the sequence of values of Z has been lost. The conflict is essentially between Janet and Janet. Stowe resolves it by putting asterisks on the halogens and (ig)noble gases, so Eric could always pop an asterisk on H (I grant that hydrides are more like halides than acids are like salts). I still vote for Valery’s transformation of Janet III, but it all goes back to Janet.
Some one sent me a picture from Science gallery in Dublin. Philip, Images of our periodic tables are displayed next to each other. I’ll send you that picture, I’ll copy Jess and Eric also.
As I mentioned to some of the people here via an E-mail it appears that the most definitive version of Stowe’s table, along with a description of it appears in an I2R calendar for 1999. The company which issued these popular chemical calendars is still in existence and I intend to call them to see what I can discover about Stowe.
I see that Stowe entitles his representation a ‘chart’. I think that word was first used by John D Clark for his spirals; tell me if I’m wrong. I think it would be a good idea to use that as the general description of tables, spirals etc. as being less clumsy than ‘representations’. I suppose it’s a bit of a stretch to push it to 3-D versions, but perhaps we can just call those ‘models’.
I will be giving a talk on my forthcoming book, “A tale of seven elements” at University College, London on the evening of August 18th, to a history of chemistry reading group organized by Professor Hasok Chang of Cambridge. I assume the meeting is open to all comers. I dont know the location but please get in touch by E-mail if you are interested in attending. eric
I took another look at the system of elements with ground state anomalies, and now wonder whether some are more ‘primary’ or prototypical than others. In the f block we have positions where we would expect f1 and f8, while in the d block instead d4 and d9. It turns out that if one maps just these to the T3 model an interesting pattern emerges. They are distributed in a radially symmetrical manner about the rotational axis of the tetrahedron. I usually orient the T3 so that H, He, Li, Be are at the very top. Remember that tetrahedra have 4 faces. The dual periods, when T3 and its subtetrahedra are oriented H-top, build up the tetrahedral structure as bent up (skew) rhombi from below, that is, the two lower tetrahedral faces. But the primary anomalies (and near neighbor anomalies) mostly occupy the UPPER two faces of the tetrahedron. Exceptions are few, unless one counts spin-orbit distortions from Janet period 8, which are on the lower two faces of a 120-sphere tetrahedron. If we also include the first-member issues from the first (1 or 2) periods containing s and p blocks, the picture is fuller. The s, p first member sets are ‘outer’ electronic structures, whose activated electronic configurations (for bonding?) may be odd (as in hybridization, or the covalent character when ionic is expected). The d, f are more internal, and their anomalous behavior is more in the ground state instead (but what about the addition of 2 s electrons here?). I’m curious what the s, p spin-orbit period 8 elements are like in this regard.
We often discuss n+l values here and on other online lists. But the anomalies/first-member deviations discussed in the first post below seem to be more about n-l instead, where the values are fixed at 1 (for odd periods) or 2 (for even). It has always puzzled me, in a universe filled with symmetry, why only n+l would be important. Might both n+l and n-l be? Could there also be some mathematical function linking them and thus forcing the mappings in a motivated fashion?
The official IUPAC periodic table is 97% in accord with quantum mechanics. Indeed, only three elements (He, Lu and Lr) are at the wrong place in the official table according to rigorous mathematical quantum mechanics (Schrödinger equation of the hydrogen atom combined with the Pauli exclusion principle without taking into account the electron anomalies) as shown in the table de described here http://bernardschaeffer.canalblog.com/archives/2008/09/23/4934243.html
Mendeleev tinkered with atomic weights to get rid of anomalies, Janet idealized shell structures to get rid of them, and the standard table does not show them at all except in the hesitation over La, Lu, Ac and Lr. We should just accept that there are things that physics cannot yet explain, but that does not mean that they are not explicable in principle.
I think there is a good deal of merit in Bernard’s suggestion. A comittment to He in the alkaline earths and placing Lu and Lr in group 3 does not necessarily commit one to a left-step table. _____________ We can stay with the conventional medium-long form while making these three changes. The only ‘loss’ is that periods are not arranged according to increasing values of n + l. ________________________So Bernard, if you claim to base yourself on QM why not also accept the left-step format? What I am trying to do here is to be clear about the difference between Bernard’s suggestions and some of the tables we have been discussing on this forum such as Janet, Stowe etc. We are all aware of the need to reconcile the periodic table with QM. The question is just how to do it. I also think that talk of 97% agreement is a little misleading given that we now know of 118 rather than 100 elements.________eric
The Figure 1: Medium-long form of the Periodic Table is 99% (approximately of course…) quantum mechanically correct. Lu and Lr are correctly below Sc and Y. Only helium is not at the right place. Indeed a vacant box waits for it above Be. Otherwise there is no difference with my table (http://bernardschaeffer.canalblog.com/archives/chimie_quantique__quantum_chemistry_/index.html). http://www.hyle.org/journal/issues/11-2/scerri.htm or http://www.hyle.org/journal/ issues/11-2/scerri_fig2.gif (I tried to paste it here without success) Bernard
If your system amounts to just a modification of the medium-long form in order to move He one should perhaps make that point more clearly instead of implying a major change, as I think you do.____________ In any case wanting to move He to group 2 places one in opposition to most chemists. Part of this debate is about whether reduction to physics can be pushed so far as to ignore chemical evidence altogether. _____ Helium sure looks like it is similar to the other noble gases in terms of chemical behavior. What right does the physicist have to tell the chemist where to place elements? _______________Is it not possible that the perfect symmetry of physics is somewhat broken at the more ‘superficial’ level of chemical behavior? Should the physicist not rather be working on some form of symmetry breaking mechanism to justify why He behaves like the noble gases in a chemical sense while really being an alkaline earth at a fundamental level? After all physicists who argue for a unification of the four forces of nature don’t just leave it at that. They look for the actual mechanism of symmetry breaking to justify the parting of the ways between the four forces at more accessible energies or at the level that we typically live at. I would be interested in comments from any or all protagonists here including Philip and Valery.
Well, if we’re going to talk about breaking symmetry and the He/noble gas issue, what about the prediction that element 118, which by right of tabular position *should* be noble, likely will not be. Here we would have spin-orbit properties outweighing others so it also will not fit in with the usual noble suspects. On the other hand, if 120 DOES turn out to be noble, again by some predictions, then it will symmetrically mirror He, if 120 is in some sense the end of the system. I’ve mentioned this more than once elsewhere, but never have gotten any satisfactory response.
There was a suggestion that element 114 behaved like a noble gas (Janet thought it might!). And how noble is Rn? And what about monatomic Hg gas? The impression is that [ig]nobility is seriously sporadic in these very heavy regions.
See http://en.wikipedia.org/wiki/Relativistic_quantum_chemistry All of a piece, with different instantiations depending on where we are in the table, including inert pair/knight’s move effect. Combine contractions with shielding, hold your breath for two moves, rinse, repeat. How many periodic properties depend on atomic size, or ionic, etc.? What about element 112? That *should* be like Hg- is it? Are there any unusual properties seen between 104 til then? I haven’t found any references to such, but have enough experiments been done on the handful of atoms often produced? What about spectra- are the data completely consistent with normal d configurations? No anomalies other than Lr at 103?
I think that similarities is somewhat subjective. A mathematical theory is not if it is experimentally verified. This is the case for the Schrödinger theory of the hydrogen atom completed by the Pauli exclusion principle. It explains rigourously the periodic table for atomic numbers less then 20 (Ca). For heavier atoms it may be seen only when the atomic levels and the electron numbers are considered. It has no incidence on the shape of the official periodic table. For elements heavier than Ca, the atomic levels are interpenetrating but it is not very important for the periodic table. This is why the IUPAC official table should be only slightly modified. The french Academy said that it is totally absurd to place He above Be and that I assaulted chemistry… The Definitive Problem of the Periodic Table seems to be now restricted to the problems of Lu, Lr, He and some exotic elements about whose very little is known. The elements 103, 104, 112, 118 are produced by a nuclear reaction. I am not sure that they may exist as atoms.
Please explain how QM augmented with Pauli’s Principle can explain the order of electron filling, in other words the n + l or Madelung rule? If there is any explanation it needs to assume the n + l rule rather than deriving it and that is not quite good enough. eric scerri
Sorry for Assaulting the French Chemists, but their position would assault Charles Janet. One day they will regret that, I am sure. There is no question that Janet’s LSPT is superior to IUPAC traditional table, simply because no satisfactory definition of a period can be provided on a basis of traditional PT.___ Eric, you are absolutely correct, QM does not explain the basis of the Periodic Table, that is n+l rule. ____ Sorry, but Chemists will have to deal with the math, because it is obvious, for at least some of us, that mathematics rules the Periodic System. It was even obvious to Mendeleev, who believed that one day there would be a mathematical theory that would explain the intricacies of the Periodic Table. IUPAC table is dead, despite the fact that so many fail to recognize it. It was first introduced in 1905 and rejected by most of the chemists then, it was revived in 1960’s, after half of century. It might take long time, but that clumsy structure will be rejected again. No doubt about that. Valery Tsimmerman.
Let us begin with hydrogen. It has only one electron usually in the fundamental level. Excited levels are normally not used but they may contain electrons. Each of these excited levels may be filled progressively with electrons. Each time an electron is added, a proton (and eventually neutrons) must also be added. The fundamental level of hydrogen may contain two electrons but it is unstable. It becomes stable if a proton (and neutrons) are added to the nucleus, giving a helium nucleus with two protons and one to ten neutrons, depending on the isotope. To obtain a He atom, two electrons have to be added around the nucleus. ___________ Each level (letter n, constant on a horizontal line for atoms lighter than Ca) contains a maximum of 0, 6, 10 or 14 electrons given by 2(2l+1) (the l should be in italics, not possible here). ______________________________________________________See figure (http://storage.canalblog.com/94/49/292736/67010620.jpg) Each sublevel contains a maximum of 2 or 4 electrons, from m = 0 to m =±l. Number l appears as a letter spdf, corresponding to 0, 1, 2, 3. It is constant in a column. _______ It is not possible to put more than two electrons in the fundamental level of hydrogen and in sublevels. This is described by the Pauli exclusion principle.____________ The fundamental level has n=1 with no sublevel: l =0. This can be seen on the figure where the elements are paired according to the Pauli exclusion principle (I am probably the first to do that)._____________ Now let us add one proton, some neutrons and one electron to obtain Li. This electron has to be at a higher level n = 2 and l =0. In this level we can put one electron more, giving Be. Then we have l =1 where we can put two more electrons. The toal number of electrons is now of 6 and so on… until Ca. Then the regularity is broken and the Schrödinger model fails as it can be seen on the figure where on the right of Ca there are two values of n, 3 and 4. The 3d subshell is lower than the 3p. In the last line, one may see, right of Ra, 3 levels 5, 6 and 7. This may be described by empirical principles or rules but it has no effect on the table which is what it is. The many presentations are probably all more or less equivalent except for the He, Lu, Lw case.__________________________________________________ All this seems somewhat complicated but it may be intuitive by observing the spherical drawings of the vibration modes of a sphere, called spherical harmonics, angular solution of the Schrödinger equation. I hope to have no mistake…
I have perhaps an explanation. According to the original theory of Bohr, the electron rotates around the nucleus and has therefore a momentum n x h_bar. According to Schrödinger, the electron has no orbital movement because he considers only a wave which is immaterial. Both theories give the same result when l=0, essentially for the hydrogen atom where the sublevels are practically not separated. The extra electrons cannot be neglected, they have a momentum l x h_bar and a total momentum (n + l) h_bar. QED! Of course it is too simple…
I disagree with Bernard’s notion that regularity exists only for the elements lighter than Ca. This is not defend Schrodinger equation, which is also an approximation, but regularity reappears after Ca on a higher level and becomes more obvious. All heavier elements, as well as elements lighter than Ca, are part of the same system that is subject to this regularity. Again, proof for such regularity is the observation made by Jess that every other alkaline earth element has atomic number equal to tetrahedral number (Be, Ca, Ba, Ubn), all other alkaline earths located between those elements have atomic numbers that are exact arithmetic means.This fact can be ignored by the science for awhile, but it can not be ignored forever.____ n+l rule is empirical rule based on spectroscopic observation. Again, it is only part of the much bigger picture that QM is not ready yet to explain. ___QM states that all quantum numbers are products of boundary conditions of Shrodinger equation, but this does not explain the interrelationship of the quantum numbers. For example they say that l=0,1,2,…(n-1), but that is not the case. n+l rule dictates that l=(n-1), (n-2),…1,0. The interplay of the quantum numbers is more complex and fascinating! Three dimensional representation of Aufbau mnemonic is the testimony of that, as demonstrated at http://www.PerfectPeriodicTable.com/novelty. This demonstrate complete regularity of the Periodic System and shows that origin of n+l rule is a part of mathematical trick known as tetrahedral packing of spheres. This principle is more basic than QM at its current state. Scientists need to look at this seriously to advance QM to the higher level. Valery.
Actinium or Activia? Anyway, in my T3 model addition of each skew rhombus of close-packed spheres, equivalent to a dual period, generates the next larger tetrahedron. For 120 elements there are 4 such tetrahedra, each complete at the tetrahedral number of spheres, therefore elements. This depicts directly in 3D idealized Aufbau with Madelung. I imagine that a good number of other 3D models do also, but with the tetrahedron it is a necessity.
Most of what you say is correct and incidentally very well known to most chemists and people interested in the periodic table. You have not addressed the one crucial point that I made. The n + l rule as Valery reminds you is empirical. The QM explanation of the periodic table does not yet extend to explaining this rule from first principles. Physicists might do well to be a little more modest therefore in explaining to us poor chemists what it is all about. Please address the theoretical status of the n + l rule.
Bernard wrote: “The extra electrons cannot be neglected, they have a momentum l x h_bar”. The magnitude of orbital angular momentum is square root of lx(l+1) times h sub bar. Not so simple.
Column: The crucible Philip Ball wonders to what extent molecular structures are metaphorical ‘Philosophy is dead’ is an assertion that, coming from most people, would be dismissed as idle, unconsidered, even meaningless. (What, all of it? Political philosophy? Moral philosophy? The philosophy of music?) But when Stephen Hawking announced this in his recent book with Leonard Mlodinow, The grand design , it was greeted as the devastating judgement of a sage and sent philosophers scurrying to the discussion boards to defend their subject (more properly, to defend Hawking’s presumed target of metaphysics). Yet many chemists may be unaware that a philosophy of chemistry existed in the first place. Isn’t chemistry about practical, tangible matters, or – when theoretical issues are concerned – questions of right and wrong, not the fuzzy and abstract issues popularly associated with philosophy? On the contrary, at least two journals (Hyle and Foundations of Chemistry) and the International Society for the Philosophy of Chemistry have insisted for some years that there are profound chemical questions of a philosophical nature. These questions might not seem quite as urgent as how to make stereoselective carbon-carbon bonds, but they should at the very least make chemists reflect about the nature of their daily craft. What is the ontological status of ‘laws’ of chemistry? To what extent are molecular structures metaphorical? What’s more, the philosophy of chemistry impinges directly on chemistry’s public image. As Eric Scerri, editor-in-chief of Foundations of Chemistry, says: ‘Most philosophers of science believe that chemistry has been reduced to physics and is therefore of no fundamental interest. They believe that chemistry has no “big ideas” to compare with quantum mechanics and relativity in physics and Darwin’s theory in biology.’1 The philosophy of chemistry excites lively, often impassioned debate. Those unquiet waters have recently been agitated by an extensive overview of the topic published in the Stanford encyclopedia of philosophy, a widely used online reference source, by Michael Weisberg, Paul Needham and Robin Hendry, all three respected philosophers of science.2 It’s an ambitious affair, accommodating everything from the evolution since ancient times of theories of matter to the nature of the chemical bond and interpretations of quantum theory. The piece has proved controversial because the authors have presented points of view on several of these issues that are not universally shared. ____________________________________Chemical conundrums Much of the debate hinges on the fact that the concepts and principles used by chemists – the notion of elements, molecules, bonds, structure, or the idea much debated by these philosophers that ‘water is H2O’ – lack philosophical rigour. Arguments about whether gaseous helium contains atoms or molecules, or whether the element sodium refers to a grey metal or to atoms with 11 protons, are frequently rehearsed. That these hardly affect the practicalities of chemical synthesis doesn’t detract from their validity as philosophical conundrums. Take, for example, Needham’s claim that isotopes of the ‘same’ element should in fact be considered different elements.3 Clearly there is rather little difference between 35Cl and 37Cl, but if ‘element’ is pinned to chemical identity, are H and D really the ‘same’? Does not even the tiniest isotope effect blur any strict definition based on chemical behaviour rather than proton number? Perhaps the Austrian chemist Friedrich Paneth was right to regard the notion of an element as something ‘transcendental’. Even more controversially, Hendry takes a view long developed by him and others such as Guy Woolley that the concept of molecular structure is mere metaphor, rendered logically incoherent by quantum mechanics. To distinguish methanol from dimethyl ether, we need to first put the nuclei in position by hand and then apply the Born-Oppenheimer approximation to the quantum equations so that only the electrons move. Without this approximation, the raw Hamiltonian for nuclei and electrons is identical for both isomers. Hendry asserts that the isomers exist as quantum superpositions, from which a particular isomer emerges only when the wavefunction is collapsed by observation. Scerri argues,4 in contrast, that this collapse happens naturally and inevitably because of environment-induced decoherence. Even if so, the image is disconcerting: molecular structures exist because of their environment, not as intrinsic entities. What of molecules isolated in interstellar space, almost a closed system? Regardless of the position one takes, it remains unclear how, or if, molecular structure can be extracted directly from quantum theory, as opposed to being rationalised post hoc – relative energies can be computed, for sure, but that’s not the same. Ultimately these questions might have answers in physics; at least for the moment, they are philosophical. __________________ Philip Ball is a science writer based in London, UK ___________ References__________ 1 E R Scerri, J. Chem. Educ., 2000, 77, 522 2 M Weisberg, P Needham and R Hendry, Philosophy of chemistry, Stanford encyclopedia of philosophy 3 P Needham, Stud. Hist. Phil. Sci., 2008, 39, 66 4 E R Scerri, Found. Chem., 2011, 13, 1 ———————————————————-
There is still an anomaly because we have 4s, 3d, 4p and also 5s, 4d, 5p. It becomes more complicated for 6s, 4f, 5d, 6p. Of course this is accounted for by Madelung’s rule which might be explained also by the packing of spheres. Similar models have been proposed, for example by Pauling. Many phenomena may be explained by various theories. I am presently trying such an approach to calculate the atomic nucleus. The magnitude of orbital angular momentum is square root of lx(l+1) times h sub bar. You are right but what is important is the projection of it along the axis of rotation. If you prefer, I can speak only of the angular momentum quantum number which is l without multiplying it by h_bar.
I am not sure to have understood what you mean by “Please address the theoretical status of the n + l rule”. Perhaps you mean that the periodic table should be presented with the s-block on the right and the f-block below for compactness. It is surely more coherent than the IUPAC table. In fact I did’nt realized that before.
The Janet [Madelung] rule is a rule of thumb with at least 20 exceptions, not a law. Why n+l and not n-l or n+something else? For that matter why do s and p electrons behave like a single set of eight? Ask an electron cloud. Electrons know how to behave even if we don’t understand why.
20 exceptions sounds like a lot, considering hundred some elements, but this means that only 20 electrons out of place. For example, La is considered as one exception, but it has 57 electrons, of which only one electron is out of place. That is less than 2%. If you take all the elements and consider misplaced electrons vs. all electrons in those elements, number of out of place electrons will be less than 1%. Thais pretty accurate for the rule of thumb.
Philip- I mentioned in an earlier posting that all the classical anomalies (in d and f) and first- (and some second) element weirdness (mostly s and p) are located in places in the system where n MINUS l= 1 (for odd periods) or 2 (for even). Gold is the obvious exception. For n+l= 7 (for odd) or 8 (for even periods) we have the more obvious spin-orbit rearrangements as for 114, 120, etc. There thus IS a numerical pattern here. We perhaps have been operating under the delusion that the ‘classical’ elements are ‘normal’. Maybe they’re NOT. In my T3 model n-l= 1,2 and n+l=7,8 form the outer 100 sphere jacket of elements surrounding an inner core of 20- the latter are all the s,p beginning with period 3 and ending in period 6 (Janet). Maybe THESE represent the normal system, with everybody else being anomalous to some extent. It all depends on whether one needs the positive number line to keep one’s sanity, or whether one is comfortable with the notions of both + and – deviations from some norm.
Jess: Your n-l is neat, but so were the epicycles that were used to fix the Ptolemaic system. The human brain has evolved to look for regular patterns, and there is always a danger that we may find regularities that do not correspond to anything fundamental.
I would like to know what are the 20 exceptions. Take a look on the Madelung column on table here (http://storage.canalblog.com/79/05/292736/67062588.jpg). The Madelung rule has no exception. The exception you cite are observed only when considering the electrons. In doing that you cannot obtain a regular table.
Philip, epicycles, as you know, were an attempt to glom several different interacting natural observable cycles into one-size-fits-all format. This reminds me, a bit, of some who try to do a similar thing with the various disparate phenomena in the PT (and I’m as guilty as any…). So we have quantum mechanics, and relativity, the oldest odd couple in the universe, each doing their individual things to produce the final interactive result. The marionette has more than one string, and apparently more than one puppeteer. But I do wonder whether the interface between relativity and QM might be far more structured and motivated than generally realized. As for the human brain and pattern recognition, sometimes the patterns seen do reflect something actually out there in the world. Just this past week there was an announcement of a study showing that young babies have a natural association with vowel qualities and sizes (sound symbolism- a topic I’ve worked with for 30 years), with nearly 100% fidelity. They haven’t yet learned to set these natural tendencies aside yet from absorbing actual acquired languages, many (but not all) of which suffer from a deplorable lack of iconic transparency, due to borrowings and cumulations of historical changes and detritus. The evidence seems to be that iconic transparency associates strongly with minimal combinatoric competency (syntax, compounding, etc.) often found with other Peircean categories such as indexes and symbols. There is some indication that the genetic system also has mixed motivation along these lines, and I’m guessing that the behaviors of individual selected elements in the PT have been ‘tweaked’ this way. Since the reason for such changes would be enhanced communication/signal processing, it becomes an open question as to WHAT is doing the communicating here….
Bernard: orbitals with lower n+l are supposed to be filled before those with higher n+l, and for equal values of n+l, orbitals with lower n are filled before those with higher n. There are twenty exceptions, starting with Cr, in which a 3d orbital (n+l=5) takes precedence over 4s (n+l=4); in La a 5d orbital takes precedence over 4f (both n+l=7 but 5>4), et ainsi de suite! Jess: I don’t think you can invoke relativity for anything lighter than Cs. But anyway, don’t we tend to think in terms of individual electrons – easier to visualize – instead of whole electron clouds?
If physics can really explain the periodic table in a fundamental manner it should be capable of deriving the n + l rule from first principles rather than just accepting it an an empirical rule. Many people have tried to do so but as I argue in the fifth of the papers listed below, they have all failed. _________________________________________________ Lowdin, P.-O., International Journal of Quantum Chemistry, 1969, S3, 331. Allen, L. C.; Knight, E. T., International Journal of Quantum Chemistry, 2000, 90, 80. Ostrovsky,V.N., Foundations of Chemistry, 2001, 3, 145. Bent, H. A.; Weinhold, F., Journal of Chemical Education, 2007, 84, 1145. Scerri, E.R., International Journal of Quantum Chemistry, 2009, 109, 959.
Valery, I don’t think your argument of saying that say only 1 electron of the 57 in lanthanum is anomalous holds much water. As we move through the elements, all attention is on the differentiating electron or electrons. eric
Philip- the ‘R’ word rears its ugly head in the PT from square one, regardless of whether it alters the gross STRUCTURE of the electronic system overtly, it DOES alter the size of the atiom, even if minimally, the electronic velocity, etc. Fine Structure Constant and all that rubbish. This means there is ALWAYS a contribution to the mix. AND, if the FSC changes from location to location, and from time to time (as some recent cosmological research seems to show), it means that the interaction between QM and relativity may be actively negotiated. Thus at least two puppeteers wrangling over who gets top billing.
Eric: you say “if physics can explain” as if physics were a static body of knowledge instead of an evolving system of tested hypotheses. In 1900 people were saying that “physics can’t explain how electrons stay in orbit”. We don’t know what the physics of the future will bring.
From the n-1=1,2 and n+1=7,8 perspective one *could* just focus on electronic effects and still see interesting patterning in the PT system, yet also miss the bigger picture. Remember there are those who wonder whether nuclear structure in some way determines electronic (and what about vice-versa??). The system of elements you can get at through normal stellar fusion processes belongs to the n-l=1,2 subset by and large, and the n+l=7,8 owns most of the unstable ones. There also isn’t a lack of hint of structure in between. Unstable 43 and 61 have a difference between them of 18 (which is Lucas and also a nice half/double square), and the difference is the same between 61 and 79, gold, so often cited for relativistic effects (even though NOT in the n-1=1,2 zone, just as 43 and 61 aren’t within n+1=7,8). 43 minus 18 gives 25, not quite at but nearly on 26, which is in the small zone where stellar fusion runs out of steam. 80Hg shows relativistic effects like 79Au, so there may be wiggle room numerically for Fe. Looking slightly more broadly wigglewise, 44 is like 76 in allowing the 8+ max. oxidation state. There are signs of all these apples and oranges effects (and others) belonging to a larger subsystem within the overall PT structure, including columnar/group and period organization. More on this geometrical solution later. JT
I never said that the lower n+l are filled before those with higher n+l. I do not consider the filling by electrons only orbitals.
And one last point: Janet thought his n+k rule (k being Bohr’s version, equal to l+1) was a law, so he altered the data on the orbitals of Cr, Cu etc to make them obey, just as Mendeleev altered RAM for Te. A good example of the importance of attending to the data!
The solution of the Schrödinger equation of the hydrogen atom gives the “spherical harmonics” schematically represented on my table with their mathematical formulas (http://storage.canalblog.com/58/52/292736/67078483.jpg). It explains rigourously the so-called periodicity’s “magic numbers”: 2 , 8, 18, 32. In fact it is 2, 8, 8, 18, 18, 32. By adding them one obtains the shell closures, e.g. the atomic numbers of the noble gases 2, 10, 18, 36, 54, 86.
I don’t see what is the problem with the JanetIII.jpg. I obtain exactly the same results wit the Schrödinger solution or more precisely with the spherical harmonics.
And yet, Bernard, a regular and consistent sequence would actually be 2,2,8,8,18,18,32,32, and the sums there would the alkaline earths, including if you will, He. WHY would nature have misplaced that first 2 in the sequence? And yet does this relate to the ability of the s orbitals to donate their electrons to bonding, as a modification of the tetrahedral sequence. At the same time, as the inert pair effect kicks in, so called nobility does seem to be less insistent. Maybe much later on one sees 6 electron additions, equivalent to a p contribution instead of s. If continued, would impossibly massive atoms get 10 and 14 electron donations to bonding? Is there a rule here, rather than an accidental, arbitrary fact?
And while I’m at it, perhaps there is something to splitting the system and saying that BOTH the traditional nobles and the tetrahedrals (ending Janet periods) are valid. Remember that in the nucleus there are TWO rather different sets of (semi)magic numbers. One set that everybody acknowledges consists of end of block structures plus first parts of orbitals split off by spin-orbit splitting. The second less-well recognized set has the end of block structures alone, at DOUBLE tetrahedral numbers. Could the electronic PT have as similarly flavored (but differently organized) split motivation? That is, the Janet periods are block enders, and single tetrahedral, but then the traditional periods end 2 moves back, subtracting out the s electrons from the Janet system. In the nuclear blocks we see an alternation of all-even and all-odd l values (that is (s/p); (d,s/f,p);(g,d,s/h,f,p)- ignoring level mixing for expository purposes. The electronic system of course has no such alternation of l values in periods for the bulk part (does it start very late??), and of course all Janet periods end in s). By moving back 2, we get traditional periods ending in p. Despite the differences, the electronic and nuclear systems do share some features, but mirror image. That is, the strong nuclear magics add electron counts beyond the (mostly) weak ones, but we have to subtract from Janet to reach the traditional periods. Is there some mathematical algorithm that can bridge the structural and count aspects between these systems? It is also curious that there may be some sort of (3+1) symmetry breaking angle here- He doesn’t fit the prevailing nobility p-block end trend, nor would element 118. Out of 8 Janet periods that’s 2 exceptions, or 2(3+1), organized symmetrically in the PT. The overall strength of nuclear (semi)magic numbers may also be built around something similar- that is perhaps 3 strong plus 1 weak at block end plus initial spin-orbit component, and 3 weak plus 1 strong at block end alone. A good number of subatomic particle phenomena seem to break into (3+1) sets, so it would be odd if this didn’t extend upwards hierarchically into atomic systems composed of these.
I don’t know Janet’s reasoning but like him, contrarily to Bohr and Coster, I don’t consider the electrons to build the periodic system. Janet table coincides mathematically with the spherical harmonics (http://storage.canalblog.com/58/52/292736/67078483.jpg). On the last line of this figure you see the series 2, 8, 18 32, all even numbers because of the Pauli exclusion principle. The number 2 is used twice; for H and He and for Li and Be. This is because the symmetry is spherical for these elements (it is also true for Na, Mg, K, Ca etc). For B, C, N, O, F, Ne, there is one plane of symmetry. Dividing by 2 to eliminate Pauli principle we obtain 3 values that are the three possibilities of orientation in space. And so we can continue for all elements without any exception. The electrons don’t exist in this model: it is entirely based on the de Broglie wave solved by Schrödinger for the hydrogen atom where there is only one electron. In fact the table desribes only the structure of the hydrogen atom. Adding electrons changes the structure because there are electric interactions between them and, therefore, changes the distribution of the electrons a little for light elements and heavily for heavy elements. Now it is always possible to take the electrons into account but it is incompatible in this type of table. It is necessary to use a table like that of Bohr and Coster.
I don’t see what you mean by tetrahedral: is it the structure of the atom or the structure of the table? I used a tetrahedral structure to calculate the binding energy of 4He and now I try to extend this model by an NaCl type crystal structure for the nucleus. Concerning the magic numbers in a nucleus, I think that it is a second order effect because the binding energy curve has only small bumps. To Jess Tauber II don’t know Janet’s reasoning but like him, contrarily to Bohr and Coster, I don’t consider the electrons to build the periodic system. Janet table coincides mathematically with the spherical harmonics (http://storage.canalblog.com/58/52/292736/67078483.jpg). On the last line of this figure you see the series 2, 8, 18 32, all even numbers because of the Pauli exclusion principle. The number 2 is used twice; for H and He and for Li and Be. This is because the symmetry is spherical for these elements (it is also true for Na, Mg, K, Ca etc). For B, C, N, O, F, Ne, there is one plane of symmetry. Dividing by 2 to eliminate Pauli principle we obtain 3 values that are the three possibilities of orientation in space. And so we can continue for all elements without any exception. The electrons don’t exist in this model: it is entirely based on the de Broglie wave solved by Schrödinger for the hydrogen atom where there is only one electron. In fact the table desribes only the structure of the hydrogen atom. Adding electrons changes the structure because there are electric interactions between them and, therefore, changes the distribution of the electrons a little for light elements and heavily for heavy elements. Now it is always possible to take the electrons into account but it is incompatible in this type of table. It is necessary to use a table like that of Bohr and Coster.
I’m referring to the abstract counts of elements in the electronic and nuclear systems, not the shapes of the orbitals or nuclei. It is interesting that while the PT can be rendered tetrahedrally the actual shapes of atoms, nuclei are generally anything but, with the exception of 4He, and the sp3 hybrid atomic orbitals. In fact it seems to me that there is some sort of pattern pressure (caused by who knows what) towards sphericality for the actual electronic and nuclear instantiations, with of course deviations from this in both areas from various causes. A sphere has the minimum surface area/volume, and can be thought of as a polyhedron with an infinite number of faces/vertices, at least in flat spacetime. By contrast, a tetrahedron has the maximal SA/V for polyhedra here. Makes you wonder if there is something behind it all. But there is also the fact that stacking of solid spheres according to Pascal’s Triangle may not be the final model here. Electrons try to avoid each other (perhaps buffered when there is a largish neutrino flux about)- in the nucleus there is supposed to be significant overlap between nucleons due to strong force interactions (so that quarks are the real issue, not free nucleons). Might the electronic system be a bit more complex than we let on? Electronic repulsion isn’t the only thing going on- remember how spin couples. What else might there be?
Hurray- yet ANOTHER numerical pattern in the PT, this one dealing with the Fine Structure Constant and the relativistic velocity of the innermost s electrons, inspired by the ongoing conversation here. First, I wanted to find out whether, when relativistic velocity and other related features (such as volume or radius change versus Bohr atom) are mapped against the PT, any obvious patterning emerged. I’ve only looked so far at relativistic velocity, so still a work in progress, but you’ll read about it here first. Now, as I’ve written many times, Fibonacci and Lucas numbers pattern nonrandomly when taken as atomic number, with the Fib preferring leftmost positions in orbital half rows, and Lucas preferring rightmost in half rows. What I found today is that if you plug in Lucas atomic numbers into Z/137, you end up with FIBONACCI percentages of the speed of light, c. That is Z=2, 1.46%c; 1, 0.73%; 3,2.19%; 4, 2.92%; 7, 5.11%; 11, 8.03%; 18,13.14%; 29,21.17%; 47,34.31%; 76,55.47%; 123,89.78%. With the actual Fine Structure Constant being more like 1/137.036, these results would be even closer to Fib percentages. Then if one takes instead Fibonacci atomic numbers to get the percent c, the results don’t immediately look related to the above. BUT, if you then take that percent c value and take THAT as an atomic number, and repeat to get percent c, you then generate a LUCAS percent c. For ex. 89/137 yields 64.96%c. So if Z=65, you get 47.44%c. IF initial Z=55, 55/137=40.15%c. Substituting 40 for the second Z, the result is 29.20 All very tantalizing, but coincidental or something deeper?
Jess, Why did you use 137? Is this because of Bohr’s assumption that it would be the last element?_____ I also made following observation this morning:_Earlier I wrote in this or previous forum that He, Ne, Zn and Yb are the elements that mark shell closures. Each of them marks closure of 1st, 2nd, 3rd and 4th shells (or K, L, M, N, if you prefer). The next closure of shell would be marked by element Uto (Z=138). Very close to Bohr’s 137. Valery.
I used Z/137 because from this one can determine the relativistic velocity of the innermost electron and other atomic properties that deviate from the Bohr atom. I don’t know what Bohr himself thought of relativistic corrections- he certainly lived long enough. As to why this should generate Fib percent light speed from Lucas numbers one only has to consider that 138 is (rounded) 100x (3-Phi), Phi being the Golden Ratio 1.618033988…, and remember how the Fiblike numbers relate to each other as ratios between series. That the end of the g-block first period ends at 138 may only be coincidental.
Why this talk of Bohr-Coster? __________ Did Coster write any papers with Bohr? If so which?__________ Coster’s claim to fame is the discovery of Hf along with Hevesy._________ eric
This talk about Bohr is because he provided a formula according to which an electron would be touching nucleus if N=137 (Annals of Physik, 71 p.266, 1923). After him Sommerfeld came up with a different formula that confirmed N=137 (1924) . ___Did Coster came up with the same result also?
2He, 10Ne, 30Zn,70Yb,138X 2-0=2=2×1 10-2=8=2×4 30-10=20=2×10 70-30=40=2×20 All differences here 2xtetrahedral numbers 1,4,10,20 But…138-70=68=2×34, NOT 35 which is the next tetrahedral number. What gives? Could restructuring of filling order fix this?
The next closure ideally for h should be at 242 (220+22). 242-138=104=2×52, NOT expected tet no. 56. But 34=35-1, and 52=56-4. The next dual period should end at Z=220+144=364, and the next orbital i should get 26 electrons, so 364+26=390. 390-242=148=2×74. 84 is the next expected tet no., and 84-74=10. So the pattern is confirmed. This means that for the first 4 period duals (leading to Z=220) when we subtract Z of one shell closure from the next, we have twice plain tetrahedral numbers 1,4,10,20. But the next set of 4 gets offset from these 2xtetrahedral numbers by successive intervals that are themselves twice the same set of tetrahedral numbers. It would be interesting if the next set of 4 after required still a third subtraction, and so on ad infinitum.
In the last post I stated that Z=220 for the end of the first 4 period duals. Sorry, I meant 120 of course. The kind of count differences I wrote about remind me of posts I made a couple of years ago on the T3 list where this sort of thing happens. I don’t remember the context.
Jess’s reasoning reminds me of Janet, who said noble gases could not be non metals because Z of the first non-metal in each period is given by the series of integers multiplied by the series of primes: thus B 1×5, Si 2×7, As 3×11, Te 4×13, At 5×17, but 6×19=114 and not 118, therefore 118 cannot be a non-metal, therefore none of the noble gases can be non-metals [and element 114 should be a non-metal?], QED. But do electrons really care about these lovely Platonic sequences?
Philip- I don’t know WHY these sequences are the way they are- they just ARE. I’ve been told that discovery of such things is NOT science, and that finding mathematical regularities in the natural world is NOT the way science is done nowadays, nor any way to get ahead in the professional realm. That is very sad, as I’ve written before. Any perusal of many arXive papers will prove the point though. People seem to prefer thought experiments, starting from assumptions (GIGO) and working the equations. So a zillion different ‘theories’ in physics today, all from PhD’s who seem totally lost motivationally. Sounds like one of those crises in the history of science. Time for a paradigm shift (or whatever they call it now)? Chemistry, OTOH, may be able to survive for the next few thousand years without any coherent theoretical treatments, as a hodgepodge collection of rules of thumb, mnemonic devices such as the ‘traditional’ PT, etc. Much more hands-on than physics (unless you’re trying to build a fission reactor in your kitchen…).
One interesting thing about the number sequences I laid out is that it does mean that 120 is in some way a natural endpoint, though not necessarily the END of elements- maybe more akin to the end of the Mayan calendrical cycle. But it also means that period 17 will also be the beginning of a new phase, not that we’ll ever get there from here. Perhaps teensy-weensy aliens living on the surface of white dwarf or neutron stars could tell us. They will possibly have a theoretical bias that tells them that elements with Z less than 121 are useless for life processes, under (their) normal physical conditions.
Thanks for the reference to the Bohr paper on 137. Coincidentally, I just started reading Arthur Miller’s book on 137 and Pauli and Jung. ____ Can you be a little more precise about the Bohr paper reference is it the English language Annals of Physics or Annalen der Physik? Also still wondering about what Coster’s role in all of this is supposed to be. As I recall it he was an experimental X-ray physicists but he may also have done some theory.
Eric, it is Annalen der Physik. ___Van Spronsen also writes about it in chapter 15 of his 1969 book.
Bohr N; Coster D X-ray spectrums and the periodic system of elements ZEITSCHRIFT FUR PHYSIK 12: 342-374 1923 NOV-JAN
I’ll look at van Spronsen to see if its the same article. There is some interesting discussion on the PT on the history of chemistry listserver. Some of you guys may find it interesting. I’m off to a philosophy of chemistry meeting in Colombia tomorrow morning. Keep up the debate!—eric
The reason for my interest in Coster is that I am currently writing about the discovery of element 72, Hf. There was a very bitter priority dispute between the Frenchman Urbain and Coster and hevesy (both working together at Bohr’s institute in Copenhagen). Much of the controversy seems to be due to naked nationalism. The British supported the French because they had been allies during the war and the Teutonic nations were still regarded as the enemy. I will be speaking about this at University College, London on Aug 18th. Details available on request.
Go to ——http://depts.washington.edu/hssexec/hss_rsch.html#listserv——————————and then go to “how to subscribe”
Denmark was neutral in World War I, so the anti-German sentiment in Britain should not have affected the dispute over Hf. But shouldn’t we call an end to this exchange? We seem to agree that ‘Janet-Stowe-Scerri’ is not the definitive PT and that’s that.
Yes Denmark was officially neutral but Bohr maintained relations with German and Austrian scientists thus making him guilty ‘by association’ in the eyes of segments of the British and French, scientific community and press.________________________. I will be documenting this in a future article.________________________________________ Philip please dont spoil the fun.______I for one never seriously thought that J-S-S was the definitive table. It’s good to have a place to discuss all these issues. As you may have seen from the recent talk on the history of chemistry forum there are few places where one can discuss philosophical aspects of the PT without going off onto too many even worse tangents and people taking offense.____________
http://www.bbc.co.uk/news/science-environment-14405122 Earth is surrounded (by antiprotons)- so REACH! Getcher hands up!
As some of you know an interesting discussion has been taking place on the history of chemistry server as to whether the idea of a ‘best’ periodic system makes any sense. Two chemists, Steve Weininger and Jay Labinger are very much against the idea. What do the people here think. If you believe that it does makes sense to talk of a ‘best’ or optimal table, please explain why. eric scerri
Maybe something along the lines of blind wise men trying to describe an elephant which they have beaten to death many times over, not to mix metaphors… Lacking the ability to project every feature of the system into our pitiful little dimensional corner of perceptible reality we are always going to be at a loss graphically. A picture may be worth a thousand words, but what do you do when you need fifty thousand? You cut corners, picks your poison, and takes your chances.
As for the subject statement, I’m not sure I agree with that completely. As I’ve posted before, recent astrophysical results seem to indicate that the Fine Structure Constant varies in space and time. Others have found that radioactive decay rates vary depending on the time of year and distance of the earth to the sun. And we all should remember that chemical/physical properties often vary depending on local environmental conditions- that is, they are context dependent. Let’s not forget that isotopes (such as H vs. D) can’t always have their chemical differences overlooked. This list of annoying facts could be vastly expanded. What is the relevance for whether there is any ‘best’ PT? People arguing for the ‘physicist’s’ versions insist that the purely quantum aspects should take precedence (which can lead to a geometrically optimal depiction such as my T3 tetrahedral model, and other similarly motivated formats). Yet relativity is always in there, mostly lurking for lower Z, but rearing its ugly head now and again, for the chemical periodic relation. For the nuclear realm, it is the 800 lb. gorilla in the room, occasionally sleeping. The ‘God’s Eye’ perspective may be complex (and orderly) enough to encompass all the seemingly disparate phenomena that seemingly militate against any easy sound bite one-size-fits-all, and maybe not. Material reality itself may self-evolve, at local or global scales. It’s a very big universe, multiverse, omniverse (you choose…). We can’t see all of it. So imagine then if you will places/times (or other (to us) unfathomable cuts) where variations of physical/chemical fundamentals (and their interactions) skew properties to such a degree that the world would be unrecognizable. I believe it would be a very great mistake to assume that the local conditions we experience are somehow central or privileged. How many times in the history of science have we been knocked off our horse in this regard? And if we aren’t in a privileged position, in space, time, mass, energy contextually, then won’t any PT depiction, based on local conditions, be distorted in some way or other? Remember what happened to Ptolemy’s cosmology, surviving as (unexamined) received wisdom for many centuries, its position bolstered by elites (more concerned with THEIR privileges and power than truth) who managed to weave it nearly inextricably into the larger fabric of religion, politics, and philosophy. The question then becomes, for me, whether we are mature enough yet to exit the world of analogues to epicyclicity and squarely face the real possibilities of multiple PT motivations, which might clash or cooperate depending on where in the system one is, and and where/when in the world one is. The truly ‘best’ depiction then might seem to be some sort of multidimensional crazy-quilt in N-dimensions.
With all the ‘Periodic Table of the XXXXXX’ out there, yet another may seem like overkill, but here goes my contribution: how about a ‘Periodic Table of the Element Synthesizing Stars’? That is, find the stellar type whose maximal Z (or range if that’s better) of production goes into the slot in the PT, its temperature, size, composition (layerwise, or internal flow patterns). Alternatively, a Hertzsprung–Russell Diagram of the Elements, showing the maximal Z produced at each point in the chart? Maybe somebody will notice a pattern beyond what is already there?
Reading on Wiki further along the lines I was proposing, I now know that ‘metallicity’, content of Z greater than 2 in stars, increases a) the further towards the center of a galaxy one goes, and b) in larger galaxies. I would imagine this also means that galaxy cores are higher in heavier elements than the periphery. Very interesting indeed. Something else that can be depicted PT-wise.
Anybody?
It is very good idea to search for a better periodic table simply because the traditional periodic system, that is “sfdp” table, requires another diagram, that is aufbau diagram, in order to teach about electronic structure of atoms. That is the sure way to confuse students. Although, some prefer it to be confusing. Why not to combine both “tools” in one? Anything wrong with Swiss Army knife approach?
Well it seems to me that Nature herself prescribes a dose of duality. For instance the incompatibility of relativity with quantum theory. ‘Fullness’ can be viewed several different ways, leading to nobility on the one hand, and LSPT alkaline earth period enders on the other. The same sort of perspective flip occurs in the nucleus. MUST there always be a single equation for real phenomena? I’m beginning to believe this is a psychological issue, not a physical one.
Although QM and GTR have not been fully unified, nobody seriously believes that there is any conflict between the two theories. Moreover, STR and QM certainly are compatible and have been unified. Relativistic calculations in chemistry are producing much valuable information. For eample one can explain why the second transition contains (6) so many more anomalous configurations as compared with the third transition series (3). In the case of the 3rd transition, relativistic effects are more pronounced such that there is more contraction and stabilization of s orbitals with the result that double occupation of s orbitals is preferred over single occupation as in the case of the six cases in the second transition. References available on request. eric scerri
When I wrote below of incompatibility, I didn’t mean to imply that one cannot utilize information from both spheres to create a composite result. Obviously Nature does it, and we can as well in calculations. What I meant is that the two theories are going to stay separate at the level of interaction that creates atoms and molecules. At a much more fundamental level, say that of String Theory if that ever proves adequate and/or viable, then ok we can perhaps get a single equation (or set thereof) that will unify both relativistic and quantum aspects. Maybe. But then atoms are at a higher level of hierarchy, and molecules higher still. I’m pretty sure that not everything manages to cross those levels without alteration, if at all. Such is the nature of a complex hierarchical system.
On one of the PBS channels we get tonight they reran a show about Fractals originally aired a few years ago (I guess before Mandelbrot’s death). It made me wonder whether anyone has looked at the electronic dynamics about nuclei from that perspective- the electron is here, then its there, then over there somewhere, which one might probabilistically model as orbitals, but in terms of occupation of spaces in times might have fractal distributions. Certainly the PT itself exhibits a number of self-similar behaviors, not only in terms of repetitions of periods into duals as well as repeats of substructures within growing periods, but also in terms of the patterning of Fibonacci and Lucas numbers taken as atomic numbers (given that the Golden Ratio is related to fractals). Anyone able to answer? Thanks.
Many popular articles and the kind that appear in Journal of Chemical Education frequently state that the periodic table is expected to end at Z = 137. The radial velocity for any particular 1s electron is supposed to be Z/137 which leads to a prediction of an upper Z of 137. But how accurate is this prediction? What are the assumptions made in arriving at this formula? Does anybody know?
See http://en.wikipedia.org/wiki/Fine-structure_constant and http://en.wikipedia.org/wiki/Talk:Fine-structure_constant
Jess, Can you please check the last website. I tried it and it failed to reach its destination. eric
Just tried it and it works for me. Sometimes Wiki pages can act up, though. If you just go to the main page you can access the talk page through a link on the top of the page
My failing memory isn’t letting me know whether I’ve asked this or not, or whether anyone else here has: From the perspective of the Janet Left-Step table, all the p6 noble gases involve two moves leftwards from the alkaline earths which mark period endings in that system. Interestingly, if one counts two steps left from Beryllium, one also ends with a noble, though s2, gas, Helium. Two steps back from Helium of course ends up at Z=0, which, while not an element except in the far abstract, does in fact partake in triad relationships as a point of origin (well, it works for Stargates anyway). Anyone remember an earlier discussion on this? Thanks.
I’ve been looking over the known set of oxidation states of the elements, and there are several interlocking patternings when the system is considered as a whole. One of the more interesting is the spread of states. No element has more than a width of 11 (Lucas numberhood relevant?). And the total range over which elements can occur is from -4 to +8, a total of 13 (Fibonacci?) positions, when 0 is included. Is there more to this? And why is oxidation favored over reduction with regard to possibilities, by a two-to-one margin? Is this also some sort of Lucas relation? That is what happens with dimensionalities in String Theory- they follow the Lucas order quite closely. And remember that Fibonacci and Lucas numbers are neither randomly nor arbitrarily placed as atomic numbers in the Periodic System. For ground states Lucas positions are almost all where one has either half or completely filled orbitals. It has been claimed by others that Fibonacci and Lucas numbers show up in stoichiometry. Might the oxidation relations be the flip side to this???
http://ericscerri.com/ comments and suggestions welcome eric scerri
Looks like there is a systematicity to Pascal Triangle analogues (where we have different outer numerical values instead of only 1’s). In the basic Pascal Triangle 1’s, then integers/natural numbers, triangulars, tetrahedral diagonals, etc., each with increasing dimensionality. Summing samplings across these (either all odd or all even dimensioned) diagonals gives the Fibonacci numbers. But if one changes one side to 2’s instead, this latter procedure generates Lucas numbers instead. But interestingly, looking at the diagonals in the Pascal analogue, what we see is 2’s, then only odd integers, then SQUARE numbers, and Square Pyramidal numbers. The dimensionality is preserved between the two Pascal systems. That is 1’s, 2’s both 0D, integers, odd integers 1D, triangulars and squares 2D (and both defined by spheres, but only the former is close-packed), then tetrahedra vs. square pyramids 3D. And so forth. All this makes me wonder whether higher outer values will shift the polyhedra/polytope bases. That is, triangular (3 sided) versus square (4 sided), etc. Would 3’s on the side use pentagons???? We now have both square pyramidal and tetrahedral Periodic System models. Would higher level analogues work as well? Is this the missing ‘Rosetta Stone’ we’ve needed?
After weeks of exploration I can now conclude that all Pascal Triangle analogues (where the numbers down the side aren’t just 1’s) are interconvertible variants of each other. In all cases the dimensionality of the diagonals remains unchanged, or so it seems so far. In addition, no matter what side numbers you start out with, these numbers provide ‘seeds’ for Fibonacci-like sequences when you sample across diagonals and then sum. My convention for listing side numbers is (X,Y), where X is the left side number, and Y the right. The seed for the left side Fib-like series is X,Y, and the seed for the right is Y,X. So for a 2,1 system, on the left we have the Lucas sequence: 2,1,3,4,7…., and on the right we have 1,2, for the Fibonacci sequence proper but starting one move ahead of the sequence using 1,1. This also means that very many different Pascal analogues generate upstream-started Fib, Lucas, and other series. For example an 8,13 Pascal. I don’t know how this might yet be relevant for the PT, but I bet it will be.
I’ve found a relation between Pascal triangle analogues and the so-called ‘metal means’. What this portends for our understanding of the periodic relation remains to be explored. At least my muse hasn’t left me entirely. Sometime I worry, esp. in dry periods. The monsoons are returning at last. See: http://en.wikipedia.org/wiki/Silver_ratio and the discussion page whose link you can click at the top of the main page- my addition appears at the very bottom of the discussion page.
Well, I worked out the first few number series whose contiguous members give Silver Ratio values. So at least these do exist. This makes me wonder whether Pascal Triangle-like figures exist for the Silver Ratio (1+squareroot2) also. If so, then are there diagonals? Anything relevant to the Periodic System?
http://blogs.nature.com/soapbox_science/2011/12/07/the-periodic-table-matter-matters ericscerri.com/
Please see
http://theoryofeverything.org/MyToE/?p=1099
For full interactivity, you will need the free Wolfram CDF Mathematica player.
Hi, there. I just want to mention something about the benefits of learning new periodic table arrangements/versions. Tsimmerman and Janet periodic tables inspired me to build a tool for easy calculation of electron configurations. It is freely accessible here.
Dr. E. Garcia
Here is another program we developed for building new tools on top of it and for mining atomic number sequences. It is not just for reproducing Janet PT atomic number sequences. The program itself was inspired in Tsimmerman’s framework. It is available here.