In many parts of the world, a freshly boiled (usually soft-boiled) egg is the crowning touch to every breakfast table, and is the very embodiment of a good start to the day. When we rap a knife on the white or brown shell of such an egg we are seldom conscious of what a technical marvel we are dealing with. Under that unpretentious eggshell (which in itself is a structural masterpiece!) is concealed, in the narrowest of spaces, a fully-fledged culinary delicacy, one that deserves very close examination.
4. An Egg’s Journey from Hen to Saucepan
The physical and chemical characteristics of a freshly laid egg change continuously during storage, due to [1]:
- Evaporation of water, such that the density of the egg—1.086 g/cm3—decreases daily by 0.0017 g/cm3, while the air pocket at the blunt end of the egg between the two shell membranes grows progressively larger;
- Release of carbon dioxide, causing the pH of the egg white to increase within a few days from 7.6 in a newly laid egg to between 8.9 and 9.4. The logarithmic scale of pH values here produces a false sense of negligibility, since the actual proton concentration is reduced to 1/60 of its original value.
This increase in pH in turn leads to a whole series of chemical changes as an egg ages. The most apparent macroscopic change is a decrease in viscosity of the originally very viscous egg-white layers. This high viscosity is a consequence of a high ovomucin content. Ovomucin, in conjunction with lysozyme, forms an insoluble protein-protein complex. As the pH rises, this complex is split apart, causing the solution to become more fluid.
Test of Freshness
From a culinary standpoint, however, it is not age alone, but also storage conditions that prove decisive.
To reliably establish the quality of an egg, it must be cracked open, permitting determination of a height in mm for the viscous egg-white layer, which in turn serves as an indirect freshness criterion (see Fig. 16).
Figure 16. Egg with its shell removed.
A standard parameter that can be calculated from this height measurement is the Haugh value: the higher the value, the fresher the egg.
![]() (1)
(1)
Strictly speaking, this simple conversion applies only to an egg weighing 56.7 g (2 oz). With lighter or heavier eggs the actual weight must be taken into account, so the calculation becomes a bit more tedious:
![]() (2)
(2)
Salmonella
Although one can always check the age of an egg by consulting the—legally prescribed!—printed label, some people are so afraid of salmonella poisoning that they refrain from consuming any soft-boiled eggs. Why is this so? Based on data released by the German Federal Institute for Risk Assessment, tests conducted on a total of 10,000 commercially distributed eggs showed that in only 0.57 % was it possible to detect Salmonella enteritidis or Salmonella typhimurium. What’s more, if these tiny culprits do turn out to be present somewhere, they will almost certainly be found to have settled on the surface of the egg.
As a rule, the contents of an egg are entirely sterile, because they are protected from attack by the shell as well as by the two outer shell membranes. Thus, the consumer should use only clean eggs, and ones that are intact and have also been kept under refrigeration. If despite these precautions a few bacteria should have settled on the shell surface, these will all be killed off anyway by the hot water used for cooking: indeed, this will occur at a temperature of 63 °C (145 °F), which of course is well below water’s boiling point. In other words, a breakfast egg, whether hard- or soft-boiled, can be enjoyed by both young and old with complete confidence.
5. An Egg in Hot Water
The art of cooking an egg actually consists of nothing more than introducing heat energy into it to such an extent, and at a high enough rate, so that—from a culinary perspective—both the yolk and the egg white will have undergone precisely the desired changes.
That sounds easier than it actually turns out to be, however. If we put an egg at a temperature T0 (for example, 4 °C, a typical refrigerator temperature) into boiling water (Tw = 100 °C), from that moment on, heat energy will be transferred through the shell to the interior of the egg. Fourier’s Law is applicable to such transferred energy:
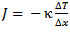 (3)
(3)
where Δx is the thickness of the shell, κ is the specific thermal conductivity, and ΔT is the temperature difference.
In this simple form, Fourier’s Law describes the heat transport per unit of surface area and time for an infinitely large and infinitely thin sheet. The essence of the law can be illustrated with an insulating pane of glass. Such a pane would be considered effective if it insulated well (κ was small), if it was thick (Δx was large), and of course if the weather outside was not extreme (ΔT was small).
It is no accident that the process necessary for describing heat transfer is referred to as “higher mathematics”. The resulting differential equations lead to easily manageable solutions only with objects of very simple form. For this reason, and for just a moment, let us proceed as if our egg were a uniform sphere, and one with no shell and no internal structure. If we were to place such a sphere with a radius a and a temperature T0 = 4 °C in boiling water (Tw = 100 °C), Fourier’s Law (Eq. (3)) offers us the following temperature distribution information [19]:
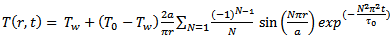 (4)
(4)
In Equations ((4)–(6)) as presented here, the authors have collected the material properties together as constants: τo = ceρa2/κ and λ = ceρ1/3/[π2κ/(4π/3)2/3], where ce is the specific heat capacity, ρ is the density, κ the coefficient of thermal conductivity, and a the radius of the sphere. The summation sign refers to addition of N terms, which theoretically can be an infinite number of terms.
Fortunately, the rather terrifying Eq. (4) can be simplified for certain practical problems. For example, the time t [min] can be calculated for which a sphere with initial temperature To and diameter d [mm], will reach a specific chosen temperature Tc when the sphere is introduced into water of temperature Tw [20]:
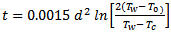 (5)
(5)
If one assumes that an egg with a diameter of 45 mm will have become hard-boiled when its center reaches 70 °C, Eq. (5) indicates a cooking time of just under 13 minutes. This value indeed corresponds to common experience with real “egg-shaped” eggs.
Hard-boiled eggs should not be cooked for too long, otherwise the white will become too hard and the yolk will be too mealy-dry, but the cooking time is certainly not as critical here as with a soft-boiled egg. In the latter case, every fraction of a minute matters. For this situation, Charles D. H. William from the University of Exeter, UK, has provided us with an approximate solution to Fourier’s Law, where the egg in question has been approximated by two concentric spheres. Thus [19]:
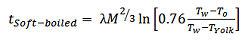 (6)
(6)
where M is the mass of the egg and Tyolk is the temperature at the yolk/egg white interface. For a soft-boiled egg, the yolk temperature should not exceed 65 °C, so according to Eq. (6) an egg taken out of the refrigerator and weighing 60 g would need to be cooked for five minutes.
Note that these cooking times are not universally valid. Extreme mountain climbers just short of the summit on the western Diamir face of Nanga Parbat who wish to fortify themselves with a couple of “five-minute eggs” would need to budget for somewhat more time. At an altitude of 7,500 m (a bit under 25,000 ft), water boils at 75 °C, so according to Eq. (5) preparation of a soft-boiled egg would require almost 12 minutes. For this reason, we would definitely advise against trying to prepare a hard-boiled egg on a mountainside due to the high risk of a sudden change in weather while you wait.
A temperature profile for egg cookery can be ascertained, at least in point-wise fashion, by the introduction of thermocouples. In a classic study [21], Richard Gardner describes in an especially witty way the conduct of an experiment in which synchronous temperature measurements were taken using two thermocouples, one in the egg white and the other in the yolk (see Fig. 17).
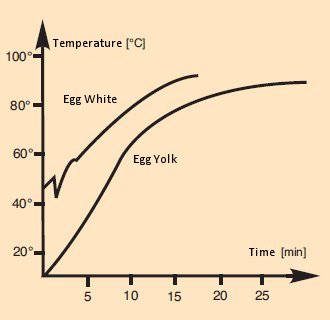
Figure 17. Changes in the internal temperature of an egg over the course of boiling.
Ignoring the instability due to a need to read just one of the thermocouples in the course of the experiment, his observations correspond at least in a qualitative way to what we might expect.
The First Non-invasive Method for Culinary Evaluation of Soft-Boiled Eggs
All the formulas so far introduced for approximation, as well as the point-wise measurements, are totally useless for the connoisseur, who would wish to know before cracking open the shell if the yolk had reached precisely the proper degree of softness—without being too runny—and if the entire white was solid, but not too hard. This poses, in the truest sense of the word, a delicate problem that mankind had been utterly unable to solve until recently.
In the course of preliminary work on this article, however, a non-destructive method for evaluating the coagulation state of a soft-boiled egg actually was developed (see Figs. 18 and 19). Now, it has finally become possible to distinguish in advance (!) between eggs accidentally or truly cooked for four and a half minutes, and ones only believed to have been cooked for the proper length of time.
Figure 18. Dr. Hans Bauer, Bayer Schering Pharma AG, Berlin, preparing six oological specimens prior to subjecting them to nuclear spin tomography (using a Siemens MAGNETOM Avanto 1.5 tesla MRI scanner).
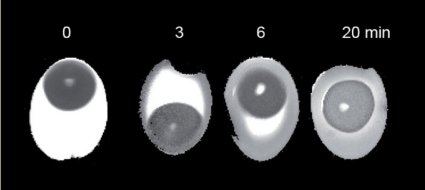
Figure 19. Nuclear tomograms of eggs boiled for various periods of time.
Nuclear spin tomography or magnetic resonance tomography (MRT) has relatively recently become a fairly standard technique for imaging in radiological diagnostics. Here the physiological object or specimen under investigation is introduced into a magnetic field, and then with the aid of short radio-frequency pulses the orientation of the nuclear magnetic fields of hydrogen atoms in the associated tissue-fluids is systematically altered, permitting an image to be calculated [22].
MRT using conventional techniques produces only very low-contrast images. However, so-called T2-images built up from a multitude of individual images have now made it possible for the first time to distinguish clearly between coagulated and non-coagulated regions in egg white. In particular, a comparison between raw, 3-minute, and 6-minute eggs shows in an impressive way the advancing egg-shaped coagulation boundary as it moves progressively toward the center (see Fig. 19).
MRT is the first non-destructive method so far developed for evaluating a soft-boiled egg in a truly reliable way. Imaging takes only 3–4 minutes, so the egg-lover need only be convinced to acquire an appropriate MRT device (current price ca. 2 million euros, or roughly $3.3 million).
References
[19] P. Roura et al., Eur. J. Phys. 2000, 21, 95. DOI: 10.1088/0143-0807/21/1/314
[20] P. Barham, The Science of Cooking, Springer Verlag, Heidelberg, Germany, 2001. ISBN 978-3-540-67466-5
[21] R. Gardner in But the Crackling is Superb: An Anthology on Food and Drink by Fellows and Foreign Members of the Royal Society (Eds. N. and G. Kurti), IOP Publishing Ltd., Bristol, UK, 1988. ISBN: 978-0750304887
[22] Klaus Roth, Chem. Unserer Zeit 1982, 16, 35. DOI: 10.1002/ciuz.200490076
[22a] Klaus Roth, Chem. Unserer Zeit 2004, 38, 348. DOI: 10.1002/ciuz.19820160203
Author
Prof. Klaus Roth
Freie Universität Berlin, Germany.
The article has been published in German in:
and was translated by W. E. Russey.
Boiled Eggs: Soft and Hard — Part 1
In Part 1 we look at what makes up an egg and how a hen produces such a marvel
Boiled Eggs: Soft and Hard — Part 3
Part 3 is devoted to experimental reproduction of the chemical highpoints of cooking an egg
Boiled Eggs: Soft and Hard — Part 4
In Part 4, we reach the practical part as we discover the ideal egg, from a culinary perspective
Other articles by Klaus Roth published by ChemViews magazine:
- In Espresso — A Three-Step Preparation
Klaus Roth proves that no culinary masterpiece can be achieved without a basic knowledge of chemistry
DOI: 10.1002/chemv.201000003 - In Chocolate — The Noblest Polymorphism
Klaus Roth proves only chemistry is able to produce such a celestial pleasure
DOI: 10.1002/chemv.201000021 - In Sparkling Wine, Champagne & Co
Klaus Roth shows that only chemistry can be this tingling
DOI: 10.1002/chemv.201000047 - In Chemistry of a Hangover — Alcohol and its Consequences
Klaus Roth asks how can a tiny molecule like ethanol be at the root of so much human misery?
DOI: 10.1002/chemv.201000074 - In The Chemist’s Fear of the Fugu
Klaus Roth shows that the chemist’s fear of the fugu or pufferfish extends as far as the distinctive and intriguing poison it carries
DOI: 10.1002/chemv.201000104 - In Chemistry of a Christmas Candle
Klaus Roth explains that when we light a candle, the chemistry we are pursuing is not only especially beautiful, but also especially complex
DOI: 10.1002/chemv.201000133 - In Pesto — Mediterranean Biochemistry
Klaus Roth uncovers the nature of this culinary-chemical marvel, and thereby comes to enjoy it all the more
DOI: 10.1002/chemv.201200001 - Video Interview with Klaus Roth




