Andrew Medford and Sushree “Jagriti” Sahoo, Georgia Institute of Technology, School of Chemical & Biomolecular Engineering, USA, and colleagues have introduced and implemented a proof-of-concept functional, PBEq, that can transition between molecular and metallic electronic environments. This functional depends on a physical parameter, denoted α, which varies in space depending on the local monopole of the electron density.

The researchers tested its performance by evaluating the formation energy of molecules, the cohesive energy and lattice constants of metals, and the adsorption energy of small surface systems, including a comparison with high-accuracy Diffusion Monte Carlo (DMC) calculations of CO adsorbed on Pt(111).

The results indicate that even a relatively simple functional with few parameters, set up based on intuition and manual analysis, performs as well or better than existing Generalized Gradient Approximation (GGA) functionals for molecular formation energies and adsorption of small molecules on metals.

 

What did you do?

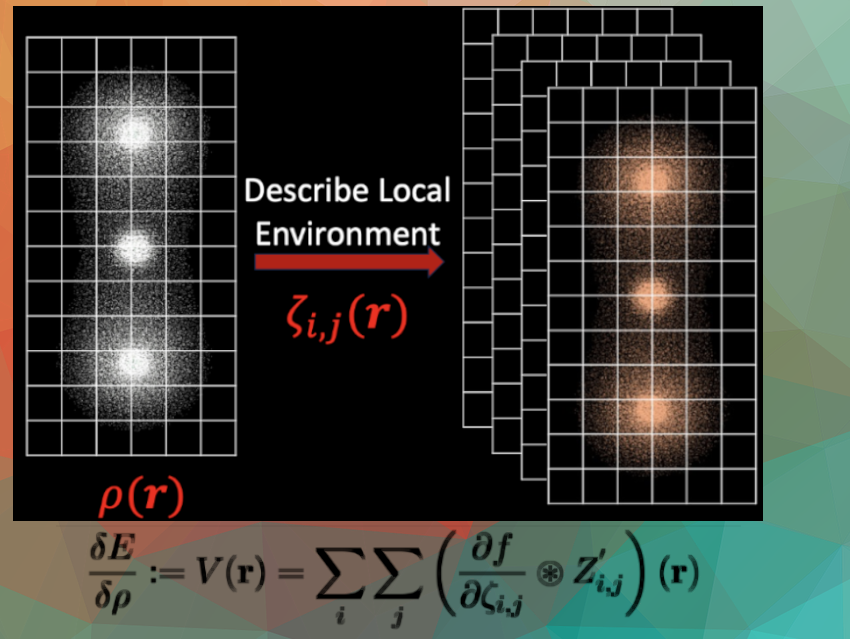
We took a new approach to an old problem. Exchange correlation functionals are the main approximation in density functional theory (DFT), one of the most widely-used techniques for quantum-mechanical simulations. Hundreds of approximations exist, but most of them use the same “ingredients”, and just change the “recipe”. We explored the idea of changing the ingredients, in a way that allowed us to mix together two existing “recipes”.

 

Why are you doing this?

When studying systems like solid catalysts, where different phases of matter (e.g., solids and gases) interact, it can be difficult to select a good exchange-correlation approximation. Our goal was to show a proof of concept for how to use the new “ingredients” to mix together “recipes” that work for solids and gases. Ultimately, we hope this helps pave the way for more advanced exchange-correlation approximations that improve the accuracy for systems relevant to catalysis.

 

What is new and cool about it?

We introduce an entire new framework for adding all sorts of new “ingredients” that can be obtained through a common mathematical technique called “convolutions”. These convolutions are commonly used in machine learning models, so the approach we present may help the development of exchange-correlation functionals that take advantage of technology originally developed for image analysis models in machine learning.

 

What is the main significance of your results?/ What are your key findings?

The main significance is that the mathematical derivation and implementation we reported enables construction of self-consistent exchange-correlation functionals from any type of input that is generated by a convolution. We found that even a relatively simple functional created with one of these new inputs gave very promising results for calculating adsorption energies of a few common systems in catalysis.

 

What specific applications do you imagine?

We hope that these functionals help pave the way for other “fused” functionals that may be useful in catalysis or other systems where there are interfaces between very different types of materials.

Longer term, we expect that the general framework of using “ingredients” obtained from convolutions will provide a foundation for a new class of machine-learned exchange correlation functionals that may be able to obtain higher accuracy at lower computational costs.

Importantly, we implemented this in the open-source DFT code “SPARC”, developed by our collaborator Professor Phanish Suryanarayana. SPARC is a fully open-source code for performing density functional theory (DFT) calculations, and it has been developed and optimized for parallelization, enabling calculations that can be performed very quickly on large supercomputers.

 

What part of your work was the most challenging?

Deriving and implementing the code for the “new ingredients” that are obtained by convolutions. Nobody had ever written those equations down before, so we had to think of clever ways to check them. Similarly, finding bugs in the code was extremely challenging because we didn’t have anything to compare to. We had to rely on a combination of intuition and numerical “sanity checks” to see if things were right.

Interestingly, one of the reviewers of the paper actually noticed something in some plots that helped us catch a bug we had missed. Fortunately, it didn’t have any impact on most of the results, but it was certainly a successful example of peer review!

 

Thank you for these insights.

 

The paper they talked about:

• Self-consistent convolutional density functional approximations: Application to adsorption at metal surfaces,
  Sushree Jagriti Sahoo, Qimen Xu, Xiangyun Lei, Daniel Staros, Gopal R. Iyer, Brenda Rubenstein, Phanish Suryanarayana, Andrew Medford,
  ChemPhysChem 2024.
  https://doi.org/10.1002/cphc.202300688