Shuttleworth Effect in Crystals (Box 2)

→ Back to Main Article

There is an essential difference between a solid and a fluid: the latter can easily rearrange under external stress (for example following the deformation of the container holding it), unlike a crystalline solid, whose atoms are linked to their neighbors by strong bonds. Therefore, if one stretches a crystalline solid, one moves its components relative to each other which may change the surface energy of the solid – something that is not possible with an incompressible liquid.

At this stage, two distinct physical quantities should be introduced:

i) the “surface energy”, γ, which represents the energy cost associated with the creation of a unit of interfacial area (for example by cutting a solid in two parts); and

ii) the “surface stress”, Γ, which represents the force (scalar here to simplify the point) necessary to increase the interfacial area by a unit of area.

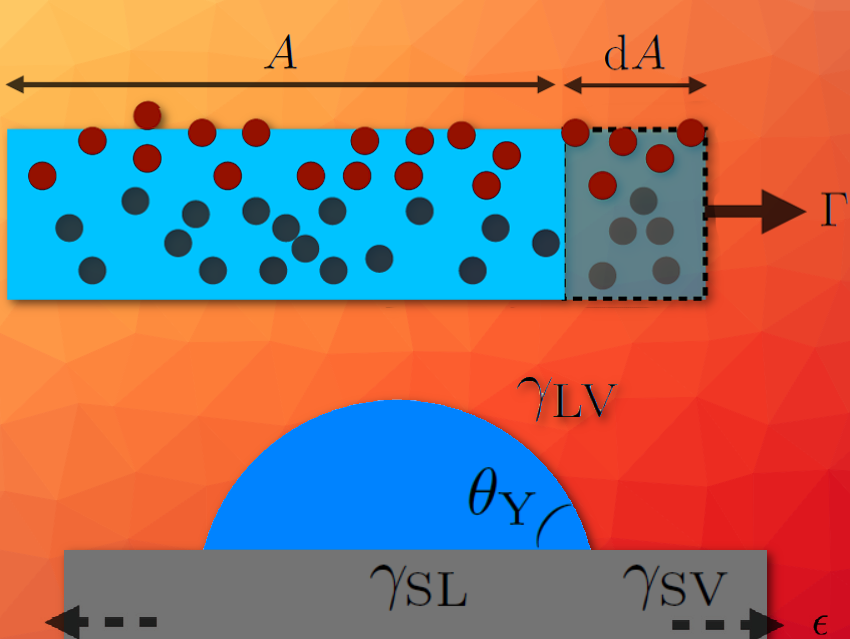
Let us now consider an interfacial area A, and an infinitesimal increase dA of the latter under the action of the external constraint Γ. A mechanical energy balance leads to equating the increase in energy d(γ A) of the interface and the external work ΓdA received by it.

In the case of an interface between two fluids, after elongation of the interface, the molecules rearrange freely and are collectively found in an average state similar to that preceding elongation (see Fig. 1a). Consequently, the surface energy γ is a quantity independent of the area A, and the previous energy balance leads to Γ = γ. In other words, “surface energy” or “surface stress” are one and the same for a fluid. We then understand the traditional usage of the ambiguous term “surface tension” and the notation γ, invariably for energy or force balances.

Figure 1a. The area A of an interface between two fluids (blue and white) is increased by an amount dA under the effect of an external stress Γ. The fluid molecules are free to rearrange despite the constraint, so that the collective situation of the molecules (red) at the interface remains unchanged, on average.

For an interface involving a solid (fully compressible here to simplify the point), things are different. After elongation of the interface, the molecules of the solid are separated further from each other. As such, the molecules are in a different state from that preceding elongation (see Fig. 1b). Consequently, γ now depends on A, and the previous energy balance leads to

Γ = γ + A(dγ/dA)

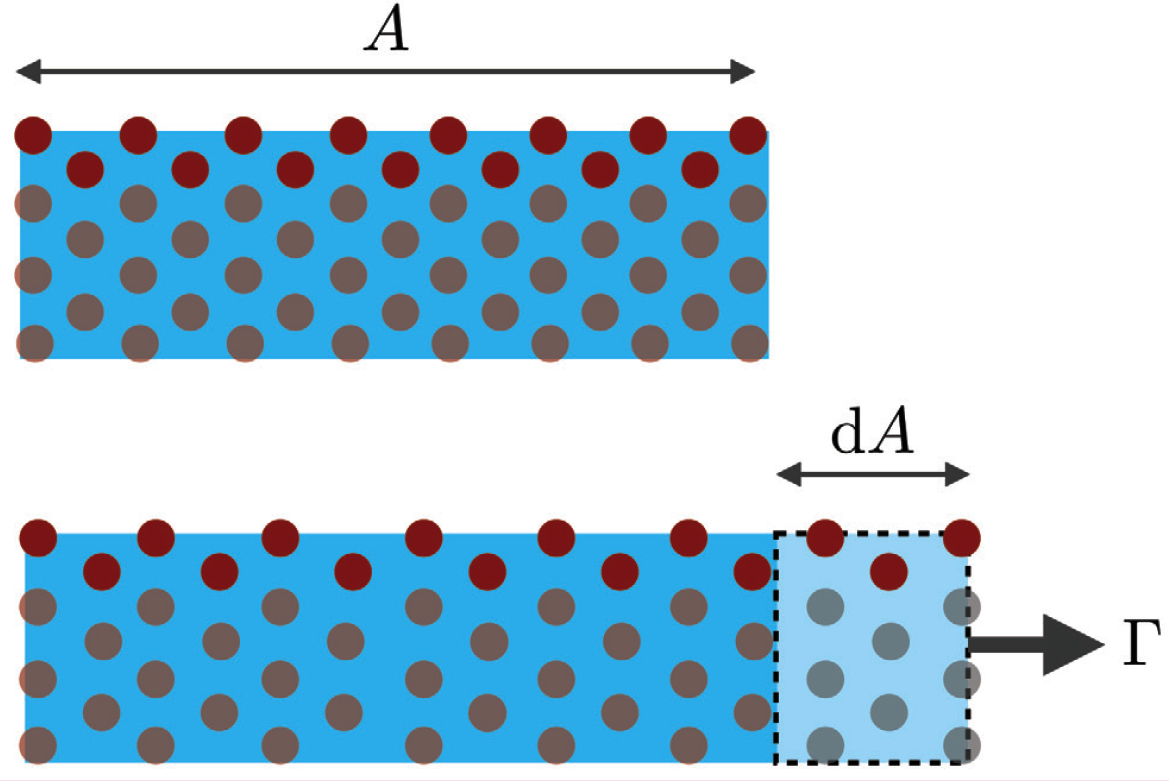
Figure 1b. The case of an interface between a fully-compressible crystalline solid (blue) and a fluid (white). Under the effect of external stress, the molecules of the crystal are separated away from their neighbors in the direction of elongation, so that the collective situation of the molecules (red) at the interface is modified.

Finally, by introducing the elastic strain ε, and its link with the increase in area, dA = Adε, one obtains the Shuttleworth relation [2]:

Γ = γ + (dγ/dε)

“Surface energy” and “surface stress” are two different physical quantities, as generally expected for energy and force in mechanics. This “Shuttleworth effect” has been extensively studied later for crystals [3], but, as these solids cannot tolerate strong elongations before rupture, there have been no major practical implications.