Is Graphene Two-Dimensional?
In 2010 the Nobel committee awarded the Prize in Physics to Andre Geim and Konstantin Novoselov “for ground breaking experiments regarding the two-dimensional material graphene”. However the debate about the real dimensionality of graphene is still open: Is it two or three-dimensional? “Some of the debate surrounds the observation that the graphene sheets are not perfectly flat but can contain waves as distortions since the carbon rings are puckered”, explains Professor Samantha Jenkins, College of Chemistry and Chemical Engineering, Hunan Normal University, China.
Euclidean Geometry
From Euclidean geometry a graphene sheet oriented in the 3-D Cartesian x-y plane is defined as being three-dimensional. This is because such a sheet has a finite extent along the x-, y- and z-Cartesian axes. Due to their “thickness” the carbon atoms have a finite extent along the z-axis, and also the sheet may contain wave-like features creating displacements of the graphene sheet along the z-axis.
Within Euclidean geometry there is the assumption that a three dimensional object will always remain three-dimensional no matter how small it is. Euclidean geometry, however, takes no account of the quantum nature of matter at the nanoscale, which renders all materials granular by virtue of having atoms as the building blocks.
For Samantha Jenkins “it became apparent that the judgment one was making on the morphology of a molecule was based purely on experience with everyday macroscopic objects”. She thinks this is surely not appropriate for these quantum mechanical objects. Looking at the topology of the electron density can be a more efficient way.
Quantum Theory of Atoms In Molecules (QTAIM)
The framework of the Quantum Theory of Atoms In Molecules (QTAIM), originated by the late Canadian chemist Richard F. W. Bader, partitions such a distribution so there are no gaps between the atoms. And it defines special points – so called ‘critical points’ – where the gradient of the total charge density distribution is zero.
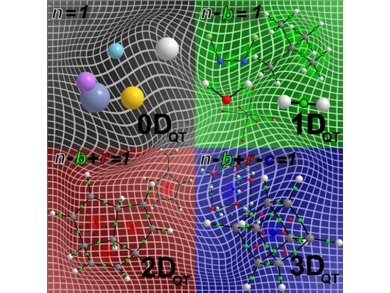
“Imagine a topographic map of a landscape with contours to represent the topology of the landscape in terms of the elevation”, says Jenkins. “The highest points on such a map are, of course, the mountain peaks where the contour lines are very closely spaced. At the bottom of wide and flat valleys the contours are very widely spaced”. In this picture, mountain peaks are compared to the nuclear positions of atoms in molecules since they have the highest local values of the charge density, thus defining ‘nuclear critical points’ (NCPs). The bottoms of the valleys can be compared to the regions, for instance, at the center of the rings in the graphene structure. Here the charge density will be a minimum, defining ‘ring critical points’ (RCPs). The path between two mountain peaks, forming a saddle shape through the lowest point between them, can be compared with the bonds in a material, or ‘bond critical points’ (BCP). Another type of critical point, the ‘cage critical point’ or CCP is a local minimum with electron density rising in all three directions of space. CCPs are located, e.g., at the geometric center of a C60 molecule. It is now easy to see how the collective set of critical points in QTAIM, along with the network of bonds, called a ‘molecular graph’, can become a powerful tool in the non-trivial past of determining the morphologies of solids, clusters, and molecules.
The presence of a CCP is, therefore, necessary for the molecule or material to be describable as “quantum topologically” in 3 dimensions, or 3-DQT. Further to this, it is easy to see that for a molecular graph the existence of a ring critical point, RCP, is necessary to be classed as having 2-DQT geometry. Similarly then, a molecular graph with no cage, CCP, or ring critical points, RCP, would be 1-DQT. The last observation was that isolated atoms only contain nuclear critical points, NCP, and are, therefore, 0-DQT.
To Settle the Debate
QTAIM can now settle the debate about whether the graphene sheet is two or three dimensional from a quantum mechanical viewpoint. The molecular graphs of graphene sheets contain nuclear, NCP, bond, BCP, and ring critical points, RCP, but no cage critical points, CCP, so the quantum geometry is quantified as being 2-DQT and not 3-DQT.
“This means that the Nobel committee was, in a way, correct in stating that the geometry of graphene is describable as two dimensional, although their judgment was not based on quantum mechanics of all of the electrons and nuclei, but on the conduction behavior of some of the electrons”, concludes Jenkins.
- Quantum topology phase diagrams for molecules, clusters, and solids,
Samantha Jenkins,
Int. J. Quantum Chem. 2013, 113 (11), 1603–1608.
DOI: 10.1002/qua.24398
This article is an adapted translation of a longer article in Chinese published at MaterialsViews China.