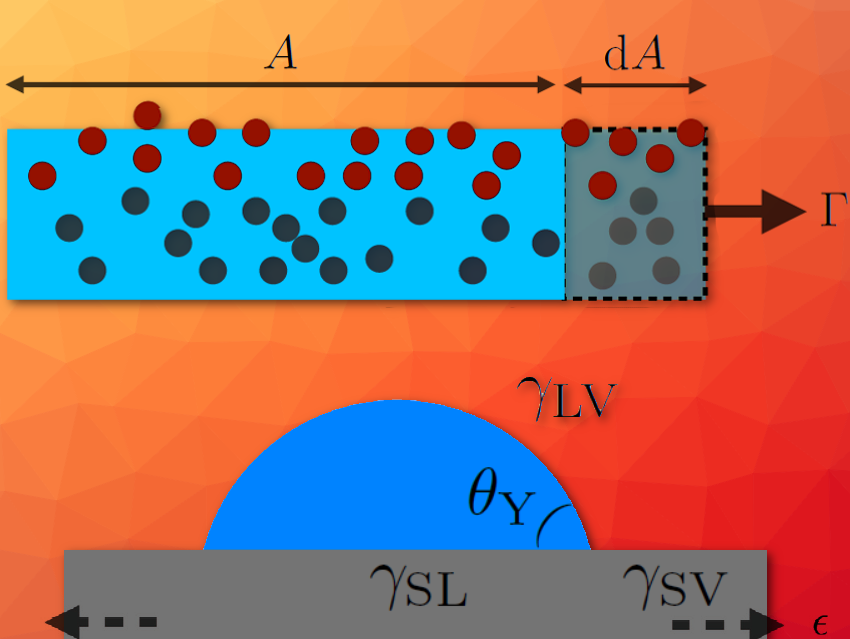
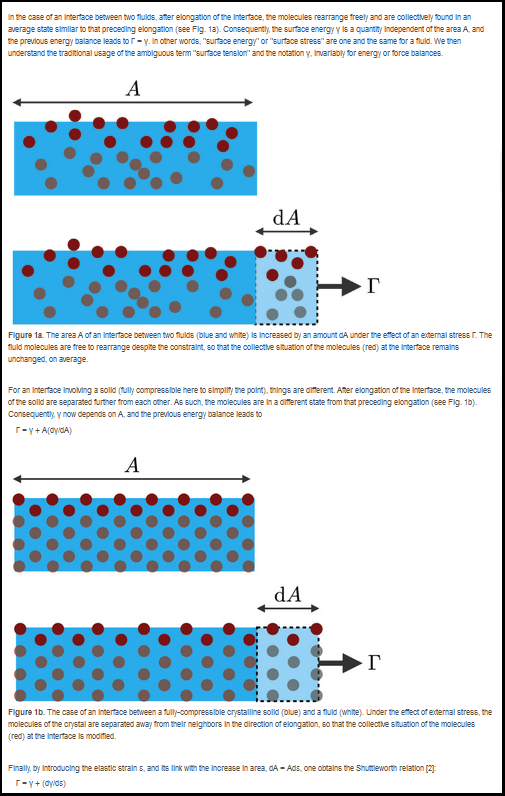
Surface stress and surface energy are physical quantities characterizing the interface between materials. Although these two quantities are identical for interfaces involving only fluids, due to the Shuttleworth effect this is a priori not the case for interfaces involving solids, since their surface energies can change with deformation. Crystals are known to show this effect, but in amorphous solids, like glasses and elastomers, the existence of this effect is debated.
In our work, we have measured and modeled the contact angle of liquid microdroplets placed on stretched amorphous solid films. We have shown that glasses exhibit strain-dependent surface energies. In contrast, our results indicate the absence of a strain-dependence for elastomers.
1 Introduction
Surface tension tends to minimize interfaces. Its microscopic origin is the affinity between identical molecules (see Box 1). In addition, by stretching a crystalline solid, one separates its constituents and then modifies its surface tension – something that is not possible with an incompressible liquid. This effect, predicted by Shuttleworth in the 1950s (see Box 2), has since been extensively studied for crystals.
Boxes 1 and 2. (click to enlarge) Capillarity and Shuttleworth effect in crystals.
There is another class of solids: non-crystalline, “amorphous” solids. This class contains two important categories for our study: elastomers and glasses. Elastomers are soft solids (for example, a car tire with an elastic modulus in the MPa range) made of long chains of polymers that are entangled but bonded to each other by a small fraction of crosslinking agents. Glasses, on the other hand, are rigid solids (for example, a plexiglas ruler of elastic modulus in the GPa range) whose constituents are not arranged periodically as in crystals, but rather in a disordered manner.
These two categories of amorphous solids typically tolerate larger deformations than crystals. Therefore, it was natural to revisit the Shuttleworth effect for glasses and elastomers.
2 Elastomers and the Shuttleworth Controversy
Elastomers have been intensely studied with the rise of soft matter at the end of the 20th century. They can be so compliant (for example, thin elastic sheets, or cosmetics and food gels) that the weak capillary forces exerted by droplets can deform them [4–7]. They may even behave like liquids themselves when their surface tension outweighs their elasticity [8–13].
Elastomers are also at the heart of a lively controversy, following a pioneering experiment carried out at ESPCI Paris, France (École supérieure de physique et de chimie industrielles de la Ville de Paris, The City of Paris Industrial Physics and Chemistry Higher Educational Institution) [14]. This study looks at a thin elastomeric wire (polyvinylsiloxane or PVS) immersed in an ethanol bath. The compression observed in the submerged part of the wire is attributed to the surface stress Γ of the solid-liquid interface. In the presence of a Shuttleworth effect, Γ has to be different from the surface energy γ (see Box 2). The non-equality between Γ and γ, and thus the existence of a Shuttleworth effect in PVS, are supported by a second analysis of the data performed by the same team [15]. However, this analysis is debated because of the liquid-like microscopic nature of elastomers (see Fig. 7).
Therefore, it has become crucial to test these ideas with independent experiments. A second team, at ETH Zurich, Switzerland, also reported the existence of a Shuttleworth effect for an elastomer [16]. Their study involves a film of crosslinked silicone oil (polydimethylsiloxane or PDMS), first stretched, and then wetted by glycerol droplets. By zooming in near the contact line, located at the junction between one droplet, the film, and the air, one observes a microscopic deformation of the film with a triangular shape. This is the “elastocapillary ridge” resulting from the balance between the capillary and elastic forces [4].
Consequently, by invoking local balances of surface constraints at this contact line, and for different deformations of the film, the ETH team concluded that the surface stress Γ of the elastomer depends on its strain ε. This could mean that a Shuttleworth effect exists in PDMS (see Box 2).
In addition, the variation of Γ derived this way appears to be remarkably large (an increase by a factor of ~ 2.5 for a change of only 25 % in the strain). This might seem inconsistent with intuition, given the microscopic origin of capillarity (see Box 1).
Collectively, these results are intriguing, and some have attributed the results to possible artifacts related to the elastomers: swelling by the liquid (like a sponge), the residual presence of free polymer chains in the solid matrix, or even altered surface properties by the presence of a rigid interfacial “crust”, etc. However, the two independent results [14,16] seem to confirm each other and no experiment is capable of directly proving the existence of such artifacts.
3 The Contact-Angle Method
Our approach, alternative to the previous ones, consists of studying the Shuttleworth effect in amorphous solids by the contact-angle method [17]. To do so, we pre-stretched glassy or elastomeric solid freestanding films, with sub-micrometer thicknesses, using a dedicated sample holder (see Fig. 1).
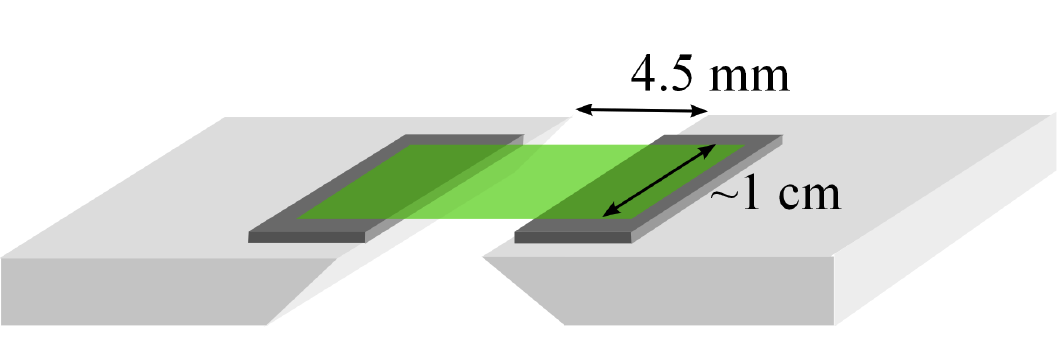
Figure 1. Schematic of the sample holder allowing for the stretching of an amorphous solid film (green) using two translating plates [17].
Once stretched, these films were transferred onto a rigid adhesive substrate. We then deposited microscopic liquid droplets on the pre-stretched supported films. For several solid-liquid pairs, we measured the contact angle θY of the droplets as a function of the deformation ε of the films (see Fig. 2). Indeed, according to Young-Dupré’s law [1], a dependence of θY in ε would imply the existence of a Shuttleworth effect (see Box 2 and Fig. 2).
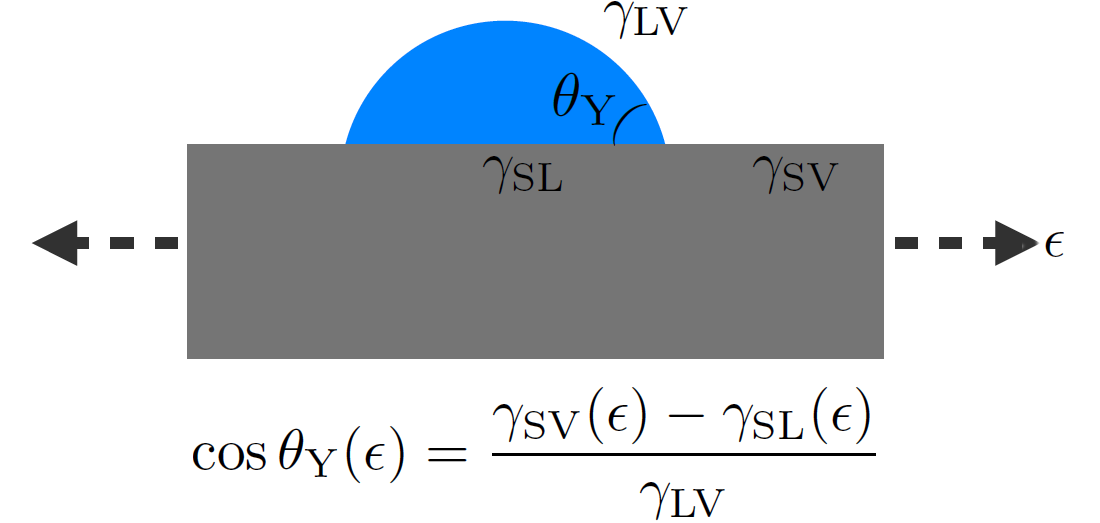
Figure 2. Schematic of the measurement principle of the Shuttleworth effect by the contact-angle method. According to Young-Dupré’s law [1] (see Box 1 Fig. 1b), the dependence of the contact angle θY of a microdroplet (blue) placed on a film (gray), with the strain ε makes it possible to probe the dependence of the surface energies with the elastic deformation.
4 Shuttleworth Effect in Glasses by the Contact-Angle Method
Let us focus first on glassy solids. Strikingly, a tiny deformation (a few percents in strain) of a glassy solid film is enough to cause a significant variation in the contact angle of the liquid microdroplet placed on it (see Fig. 3).
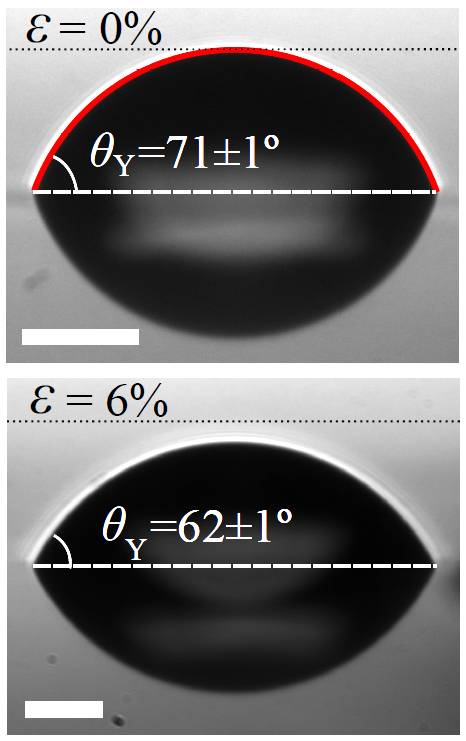
Figure 3. The contact angle of a liquid microdroplet on a glassy film at rest (top), and slightly stretched (bottom), measured by adjusting the profile with a spherical cap (red). The scale bar is 50 microns. Please note that the image of the microdroplet is reflected by the glassy film [17].
According to Young-Dupré’s law [1], this implies a variation in the difference between the surface energies of the interfaces involving the solid. This is seen for four different liquid-solid pairs (see Fig. 4, black dots).
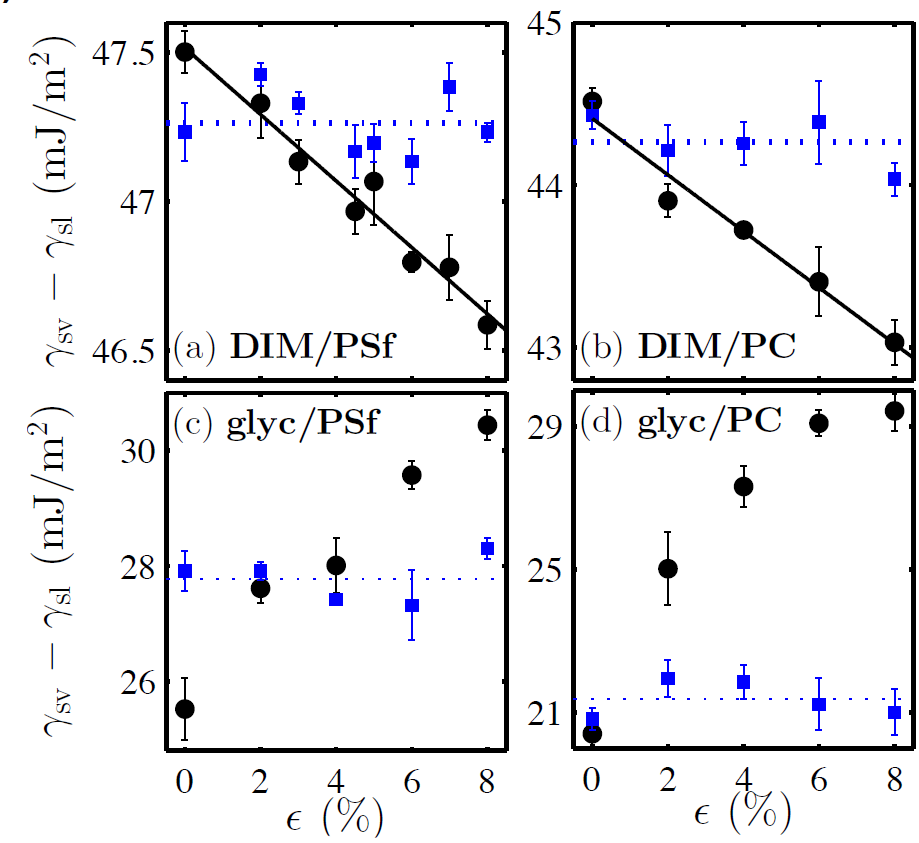
Figure 4. The difference of the surface energies of the solid as a function of the elastic strain (black dots), obtained from the measurement of the contact angle and the Young-Dupré law [1] (see Fig. 2).
The results are shown for four liquid-solid pairs involving two liquids, diiodomethane (DIM) and glycerol, and two glasses, polysulfone (PSf) and polycarbonate (PC). The solid black lines come from the theoretical model which simply takes into account the average molecular spacing in the calculation of the surface energy (see Box 2). The glassy film corresponding to each measurement point is subsequently heated above its glass-transition temperature, then quenched back, and a new measurement is performed (blue squares) [17].
In addition, we have developed a model considering only the increase of separation between the molecules of the solid induced by the elongation, and therefore the associated change in surface energy (see Box 2). This model correctly captures the trend seen in the experimental data (see Fig. 4, black lines).
Finally, melting the stretched film above its glass-transition temperature to relax the elastic stresses, and then quenching it again before depositing a new microdroplet on it, allowed us to recover a result consistent with that obtained in the absence of elongation (see Fig. 4, blue squares). Therefore, we have proved for the first time the existence of the Shuttleworth effect in glasses.
5 Shuttleworth Effect in Elastomers by the Contact-Angle Method
Unlike the case of glasses, our study reveals that a large deformation (doubling of the length) of an elastomeric substrate does not cause any measurable variation in the contact angle of a liquid microdroplet placed upon it (see Fig. 5). This implies that the Shuttleworth coefficients dγ/dε are identical for the solid-vapor (SV) and solid-liquid (SL) interfaces (see Fig. 2 and Box 2), for a wide range of strains. Furthermore, since this identity holds for several different fluids on the same solid (see Fig. 6), we are led to conclude that the Shuttleworth coefficient is independent of the fluid placed on the solid.
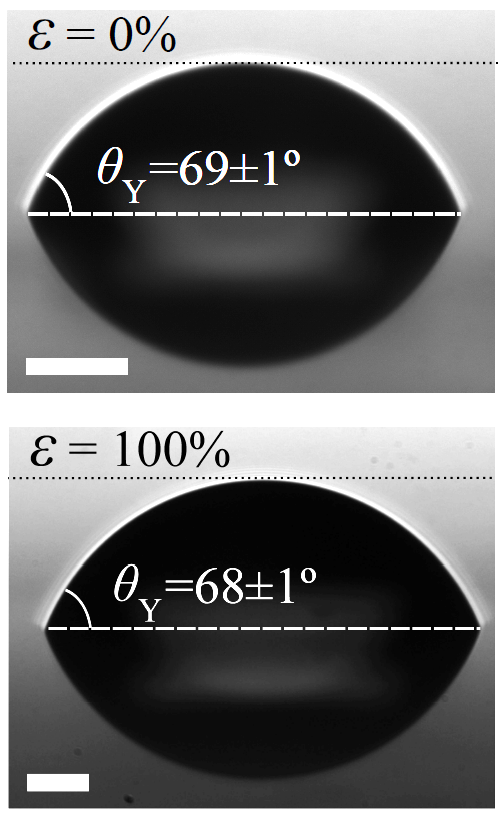
Figure 5. The contact angle of a liquid microdroplet on an elastomeric substrate at rest (top), and very stretched (bottom). The scale bar is 50 microns. Note the image of the microdroplet reflected by the film [17].
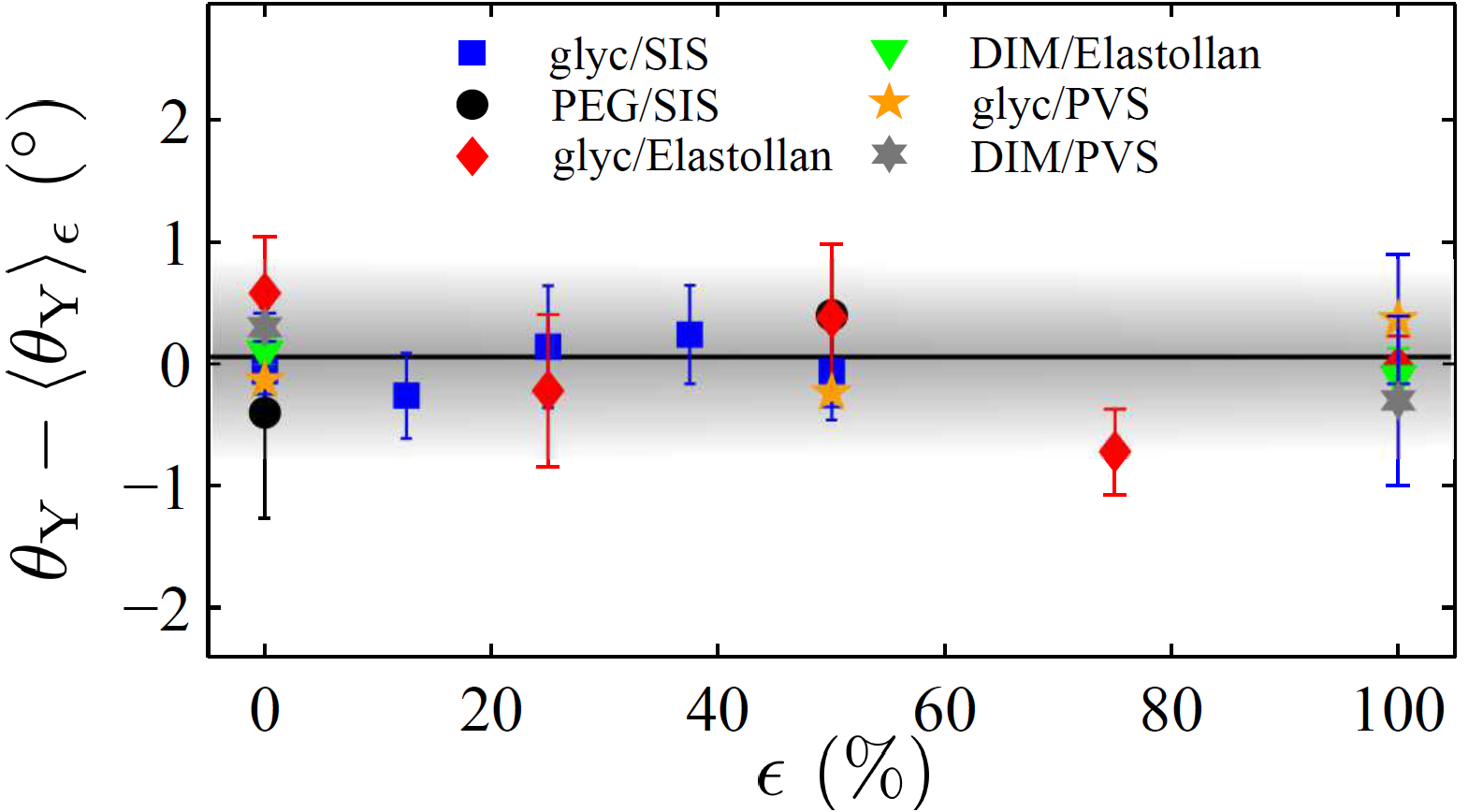
Figure 6. Deviation of the contact angle from the mean of the measured values as a function of elastic strain, for six liquid-solid pairs involving three liquids (polyethylene glycol (PEG), DIM, and glycerol) and three elastomers (PVS, Elastollan, and styrene-isoprene-styrene (SIS)) [17].
Such a statement with a finite Shuttleworth coefficient seems physically unlikely, given the microscopic origin of capillarity (see Box 1 and Box 2). We thus suggest that the Shuttleworth coefficient is null, i.e. that there is no Shuttleworth effect in pure and homogeneous elastomers.
Our result seems to contradict those of the two previous experiments [14,16]. It is however confirmed by a molecular-dynamics study carried out by a team from the University of Akron, OH, USA [18]. In this numerical study, connected assemblies of beads and springs simulate cross-linked polymer chains. Naturally, the interactions between beads are calibrated beforehand so that the numerical model reproduces well the physics of elastomers. Then, by stretching these model elastomers, the team from Akron was able to calculate the surface stresses numerically and verified that there is no notable Shuttleworth effect – at least within the typical deformations of experiments.
This conclusion agrees well with our results and intuition based on the microscopic structure of an elastomer (see Fig. 7): the latter is essentially a liquid, therefore, without the Shuttleworth effect (see Box 2), but weakly connected by a small fraction of crosslinkers.
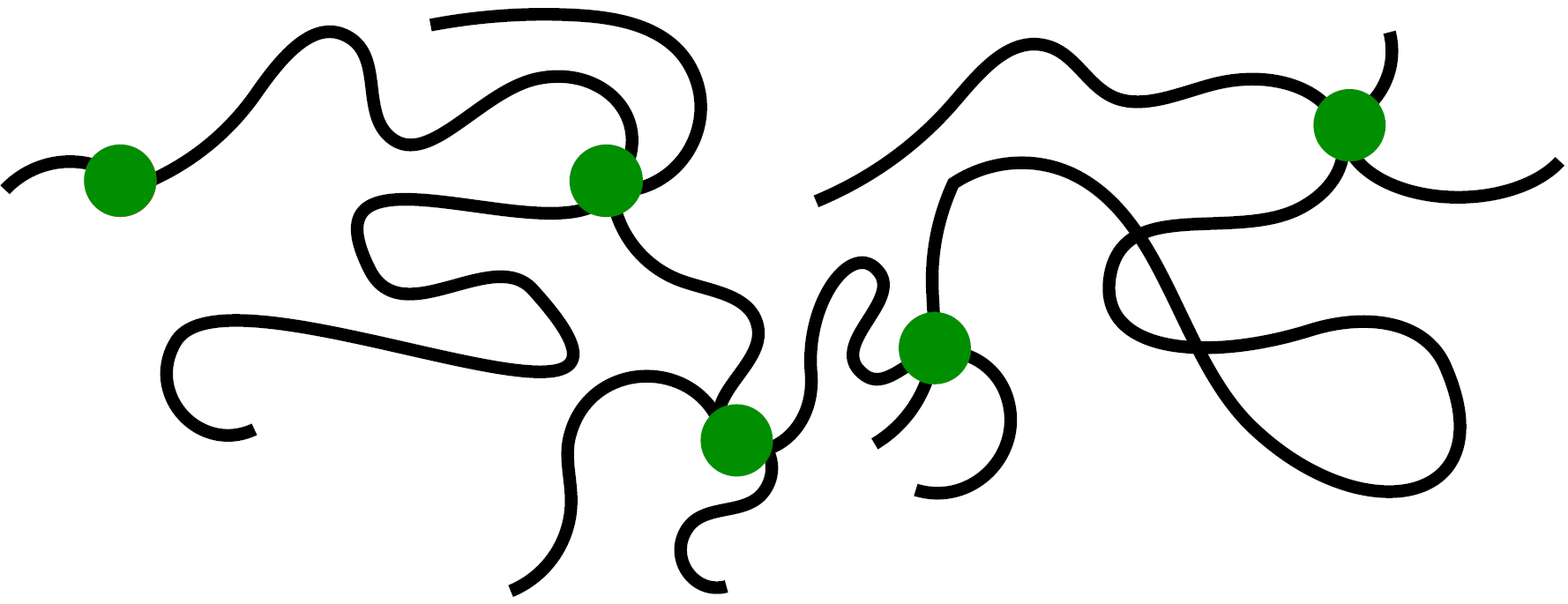
Figure 7. Schematic of the microscopic structure of an elastomer: Polymer chains (black) are freely entangled but irreversibly connected by a small fraction of crosslinking agents (green).
6 A Stubborn Enigma
The controversy persists and it even develops, as illustrated by two recent theoretical results that are opposed in some of their conclusions. On the one hand, there is a calculation based on linear elasticity [19] by the ESPCI authors of the pioneering experiment (see Chapter 2; [14]). Under certain assumptions – in particular small deformations in the elastocapillary ridge and the absence of wetting hysteresis and thus defects – this work seems to indicate that it is normal not to detect a Shuttleworth effect in elastomers by the contact-angle method [17], even if this effect does exist.
On the other hand, there is a result of a team from Paris Diderot University, France, based on a model of non-linear elasticity and involving an intriguing analogy with the defects in crystals [20]. This work seems to indicate that the Shuttleworth effect is not necessary to explain the results of the ETH Zurich team [16]. This finding can then agree with the thesis that such an effect does not exist in elastomers. The difficulty in resolving this controversy likely lies in the fact that the various experiments [14,16,17] and models [14–20] do not address exactly the same physical observables, nor the same materials, or do not rely on the same laws.
7 Outlook and Applications
In summary, the question is far from being resolved, and new independent studies will be needed. Ideally, they will measure the surface energy γ of a single solid-fluid interface in absolute terms as a function of the strain ε of the solid (see Box 2) for all of the solid-liquid pairs tested so far. In addition, using neutrons or X-rays, having access to a fine characterization of the surface of the PDMS used by the ETH team [16] would help to answer certain questions on the homogeneity of this important material and the suggested presence of a rigid interfacial “crust”.
Nevertheless, regardless of the microscopic surface structure of PDMS, the fact remains that it is widely used worldwide and that it shows some characteristics which indicate a significant effective Shuttleworth effect [16]. In addition, the existence of a Shuttleworth effect in glasses seems to be proven [17]. We can, therefore, imagine controlling the wetting properties of a plastic material by simply stretching it. From fog-harvesting nets to smart textiles and surface treatments, the number of potential applications is very high.
Acknowledgments
These work and thoughts are the fruit of several important discussions with Jacco Snoeijer, Robert Style, Eric Dufresne, Anand Jagota, Herbert Hui, Stefan Karpitschka, Bruno Andreotti, Frédéric Restagno, Qin Xu, and Nicolas Bain. The authors warmly thank them, as well as Jean-Pierre Foulon and Vera Koester for their detailed comments on the manuscript. Finally, the authors thank Patricia Pineau, Séverine Bléneau, Gilberte Chambaud, and Roselyne Messal for their help on the French version of this article in L’Actualité Chimique [21].
References
- Thomas Young, An essay on the cohesion of fluids, Phil. R. Soc. London 1805, 95, 65. https://doi.org/10.1098/rstl.1805.0005
- R. Shuttleworth, The surface tension of solids, Proc. Phys. Soc. London Sec. A 1950, 63, 444. https://doi.org/10.1088/0370-1298/63/5/302
- Pierre Müller, Andrés Saúl, Elastic effects on surface physics, Surf. Sci. Rep. 2004, 54, 157. https://doi.org/10.1016/j.surfrep.2004.05.001
- M. E. R. Shanahan, The influence of solid micro-deformation on contact angle equilibrium, J. Phys. D: Appl. Phys. 1987, 20, 945. https://doi.org/10.1088/0022-3727/20/7/018
- B. Roman, J. Bico, Elasto-capillarity: deforming an elastic structure with a liquid droplet, J. Phys.: Condens. Matter 2010, 22, 493101. https://doi.org/10.1088/0953-8984/22/49/493101
- R. D. Schulman, A. Porat, K. Charlesworth, A. Fortais, T. Salez, E. Raphaël, K. Dalnoki-Veress, Elastocapillary bending of microfibers around liquid droplets, Soft Matter 2017, 13, 720. https://doi.org/10.1039/C6SM02095J
- R. D. Schulman, R. Ledesma-Alonso, T. Salez, E. Raphaël, K. Dalnoki-Veress, Liquid droplets act as “compass needles” for the stresses in a deformable membrane, Phys. Rev. Lett. 2017, 118, 198002. https://doi.org/10.1103/PhysRevLett.118.198002
- S. Mora, T. Phou, J.-M. Fromental, L. M. Pismen, Y. Pomeau, Capillarity driven instability of a soft solid, Phys. Rev. Lett. 2010, 105, 214301. https://doi.org/10.1103/PhysRevLett.105.214301
- R. W. Style, C. Hyland, R. Boltyanskiy, J. S. Wettlaufer, E. R. Dufresne, Surface tension and contact with soft elastic solids, Nat. Com. 2013, 4, 2728. https://doi.org/10.1038/ncomms3728
- T. Salez, M. Benzaquen, E. Raphaël, From adhesion to wetting of a soft particle, Soft Matter 2013, 9, 10699. https://doi.org/10.1039/C3SM51780B
- C. T. Hui, T. Liu, T. Salez, E. Raphaël, A. Jagota, Indentation of a rigid sphere into an elastic substrate with surface tension and adhesion, Proc. Math. Phys. Eng. Sci. 2015, 471, 20140727. https://doi.org/10.1098/rspa.2014.0727
- A. Chakrabarti, A. Porat, E. Raphaël, T. Salez, M. K. Chaudhury, Elastowetting of soft hydrogel spheres, Langmuir 2018, 34, 3894. https://doi.org/10.1021/acs.langmuir.8b00368
- B. Andreotti, O. Bäumchen, F. Boulogne, K. E. Daniels, E. R. Dufresne, H. Perrin, T. Salez, J. H. Snoeijer, R. W. Style, Solid capillarity: when and how does surface tension deform soft solids?, Soft Matter 2016, 12, 2993. https://doi.org/10.1039/C5SM03140K
- A. Marchand, S. Das, J. H. Snoeijer, B. Andreotti, Capillary pressure and contact line force on a soft solid, Phys. Rev. Lett. 2012, 108, 094301. https://doi.org/10.1103/PhysRevLett.108.094301
- B. Andreotti, J. H. Snoeijer, Soft wetting and the Shuttleworth effect, at the crossroads between thermodynamics and mechanics, Europhys. Lett. 2016, 113, 66001. https://doi.org/10.1209/0295-5075/113/66001
- Q. Xu, K. E. Jensen, R. Boltyanskiy, R. Sarfati, R. W. Style, E. R. Dufresne, Direct measurement of strain-dependent solid surface stress, Nat. Com. 2017, 8, 555. https://doi.org/10.1038/s41467-017-00636-y
- R .Schulman, M. Trejo, T. Salez, E. Raphaël. K. Dalnoki-Veress, Surface energy of strained amorphous solids, Nat. Com. 2018, 9, 982. https://doi.org/10.1038/s41467-018-03346-1
- H. Liang, Z. Cao, Z. Wang, A. V. Dobrynin, Surface stress and surface tension in polymeric networks, ACS Macro Lett. 2018, 7, 116. https://doi.org/10.1021/acsmacrolett.7b00812
- J. H. Snoeijer, E. Rolley, B. Andreotti, Paradox of contact angle selection on stretched soft solids, Phys. Rev. Lett. 2018, 121, 068003. https://doi.org/10.1103/PhysRevLett.121.068003
- R. Masurel, M. Roché, L. Limat, I. Ionescu, J. Dervaux, Elastocapillary ridge as a noninteger disclination, Phys. Rev. Lett. 2019, 122, 248004. https://doi.org/10.1103/PhysRevLett.122.248004
- Thomas Salez, Déformer un solide modifie sa mouillabilité… ou pas !, L’Actualité Chimique 2020, 451, 34. Link
Authors
- Thomas Salez (Email: [email protected])
.gif)
Univ. Bordeaux, CNRS, LOMA, UMR 5798, 33405 Talence, France.
Global Station for Soft Matter, Global Institution for Collaborative Research and Education, Hokkaido University, Sapporo, Hokkaido 060-0808, Japan. - Rafael D. Schulman
Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, ON L8S 4M1, Canada. - Miguel Trejo
.gif)
UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, 75005 Paris, France.
Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Física, Instituto de Física de Buenos Aires (IFIBA-CONICET), Ciudad Universitaria, Buenos Aires 1428, Argentina. - Elie Raphaël
.gif)
UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, 75005 Paris, France. - Kari Dalnoki-Veress
.gif)
Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, ON L8S 4M1, Canada.
UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, 75005 Paris, France.
The article has been published in French as:
- Déformer un solide modifie sa mouillabilité… ou pas!,
Thomas Salez,
L’ACTUALITÉ CHIMIQUE 2020, 451, 34-38.
Link
and was translated by the authors.