Emil Fischer's Unsolved Case: Cleared Up after 120 Years

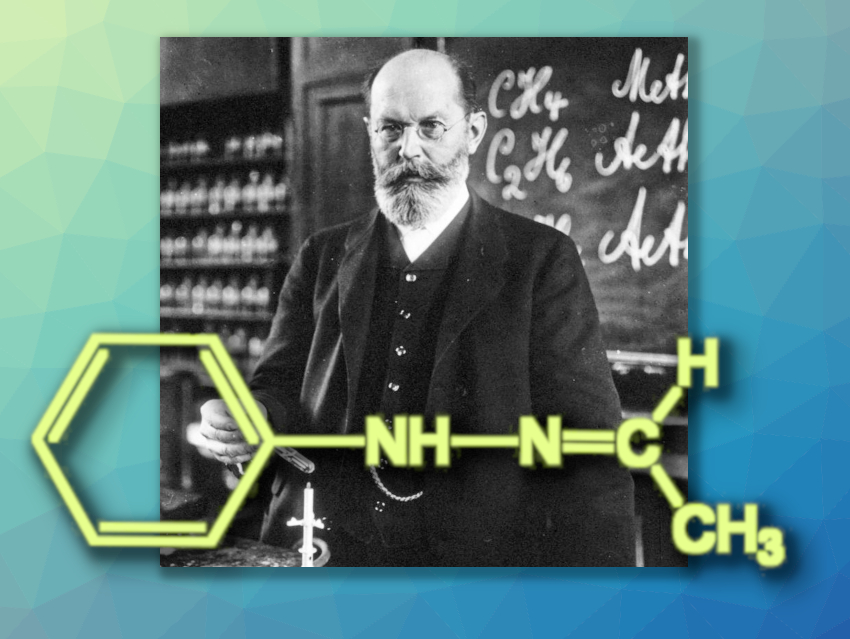
The chemical puzzle of Fischer’s tricky hydrazone that we introduced in Part 1 of this article continues: It was not possible to explain the unusual melting behavior of the two crystal forms with the measurement techniques available in 1905. The case was abandoned and Fischer’s unsolved case finally faded from memory.

2. Fischer’s Hydrazone 2.0

In 2008, British chemist Terry Threlfall stumbled across Fischer’s 1897 publication [3]. As an industrial chemist, he was very familiar with even the most peculiar of crystallization processes [13] but he could not make heads nor tails of the tangle around Fischer’s hydrazone. Curious, he repeated the old procedures, convinced himself that the melting points did indeed fluctuate, and began by sifting out the certain parts of the puzzle around Fischer’s hydrazone:

1. Fischer’s hydrazone crystallizes in two crystal forms.
2. Both crystalline forms precipitate upon recrystallization from ethanol: the α form in the presence of trace amounts of base; the β form in the presence of trace amounts of acid.
3. The α form melts at 100 °C; the β form at 58 °C.
4. Both crystalline forms liquify without decomposition to give the melted hydrazone.

The ability of one compound to form two different crystalline forms is known as polymorphism (poly (Greek) = many; morphe (Greek) = form) and is relatively common. Polymorphism was discovered in inorganic compounds like elemental sulfur and some salts by Mitscherlich [14]. In 1832, Liebig and Wöhler were the first to observe this phenomenon in an organic compound, benzamide [15].

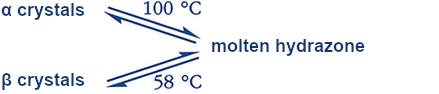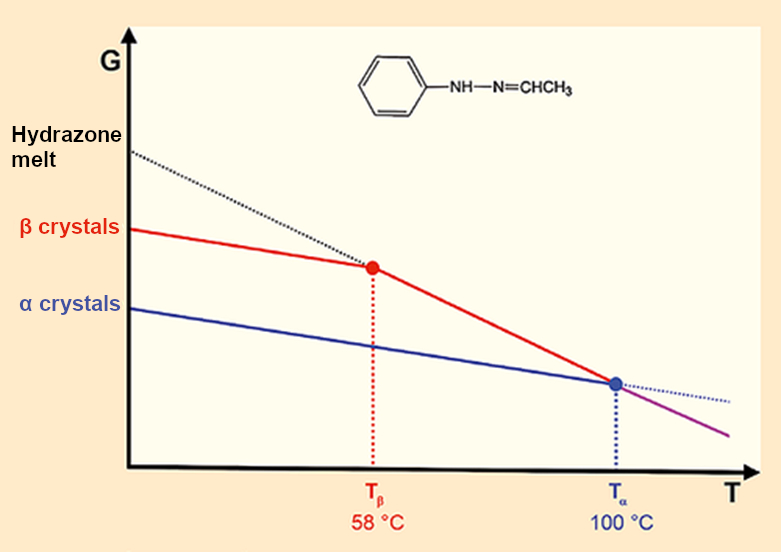
Polymorphic crystals differ in their structure, crystalline form, and melting point but always lead to identical melts. The thermodynamics are clear (see Fig. 3). As the temperature increases, the energies of the solid and liquid phases decrease. At the relevant intercepts, the melting points, liquid and solid phases are in equilibrium (ΔG = 0).

Figure 3. Fischer’s Hydrazone: Two crystals – two melting points – one melt

This thermodynamic clarity is deceptive, because the unpredictable properties of the two crystalline forms of Fischer’s hydrazone, with their interconversion and unpredictable melting behavior, remained unexplained. To solve this puzzle, Terry Threlfall was joined in a collaboration by colleagues from England, the Netherlands, and Portugal.

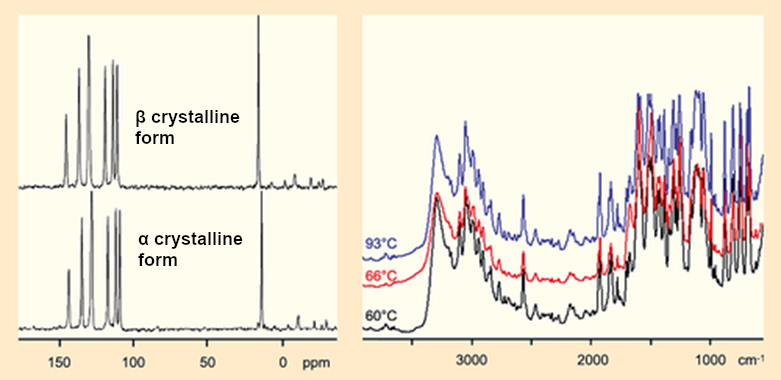
13C NMR spectra and infrared spectra of the two crystalline forms of Fischer’s hydrazone look suspiciously similar (see Fig. 4).

Figure 4. NMR and IR spectra of the α and β crystals.

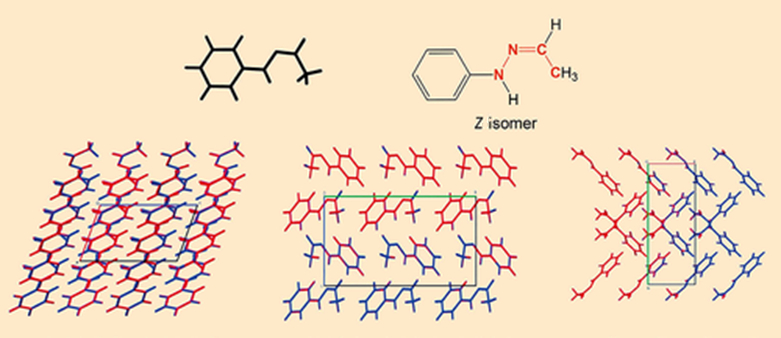
To discover more about their structure, X-ray crystal structure analyses were carried out for both crystalline forms (see Fig. 5). Surprisingly, all of the hydrazone molecules in both crystalline forms are in the Z configuration. (In the Z configuration, the substituents with the highest ranking on each of the two atoms of the C=N double bond, i.e., –CH₃ and –NH–C₆H₅, are on the same side of the double bond; Z is from the German word zusammen, meaning together).

This was not expected, because the Z isomer should be less energetically favorable than the E isomer due to the steric hindrance between the methyl group and the cis-oriented C₆H₅–NH– substituent on the C=N double bond [16].

Figure 5. X-ray crystal structure analysis of the α and β crystalline forms.

The real shocker from the X-ray crystal structure analysis was that it confirmed the spectroscopic findings that the α and β crystalline forms are completely identical.

Let us add two new items to our list of puzzle pieces:

5. Puzzle piece 1 is false, the opposite is true: Fischer’s hydrazone crystallizes in a single crystalline form.
6. In the crystal, all molecules are in the Z form.

2.1. The Dilemma Begins

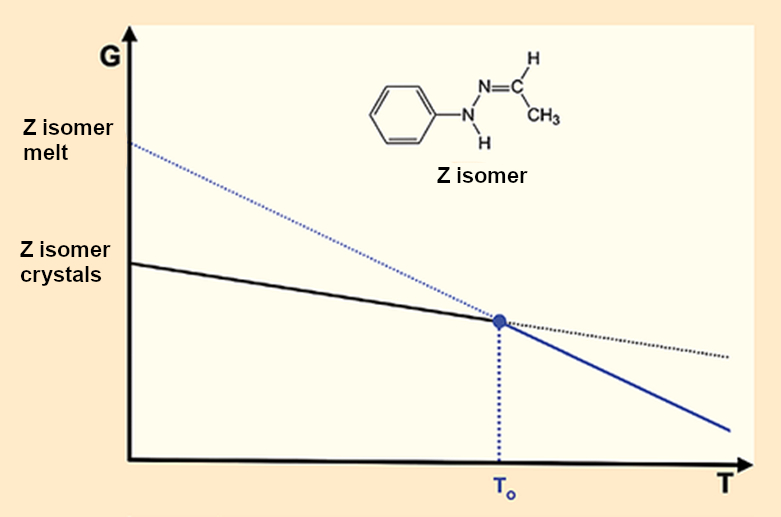
As happy as we are about the capabilities of modern spectroscopy and X-ray crystal structure analysis, they only bring us great misery when it comes to Fischer’s hydrazone. The missing second crystalline form simplifies the corresponding melting diagram (see Fig. 6) but leads to a huge problem. If there is only one crystalline form (see puzzle piece 5) that leads to a single melt (see puzzle piece 4), it is only possible to have one melting point. End of discussion.

7. If puzzle piece 5 is correct, meaning that there is only a single crystalline form, then there can be only one melting point, which means that puzzle pieces 2 and 3 are false.

Our puzzle pieces somehow do not seem to fit together. We definitely would not have a problem calling the existence of the α and β crystals a mistake that was now corrected after a long time. However, both of the crystalline forms can still be made by the old procedures to this day, in hundred-gram amounts. Two glorious, white, crystalline powders that unquestionably melt at 58 °C and 100 °C, thermodynamics or not.

For Fischer’s hydrazone, laboratory work now stood on one side, while thermodynamics and analytical measurement methods stood on the other, irreconcilably opposed. Terry Threlfall said [17]:

“We were then faced with having the dilemma between re-writing the thermodynamics laws of the universe or disbelieving the evidence of our own eyes.”

In a scientific dilemma, it is best to doubt everything that seems to be certain, both the laboratory findings and thermodynamics. As a practitioner, Fischer clearly had preferences [18]:

“One is strongly warned about letting oneself be influenced by theories or other preconceived opinions when observing phenomena or carrying out analyses and other determinations.”

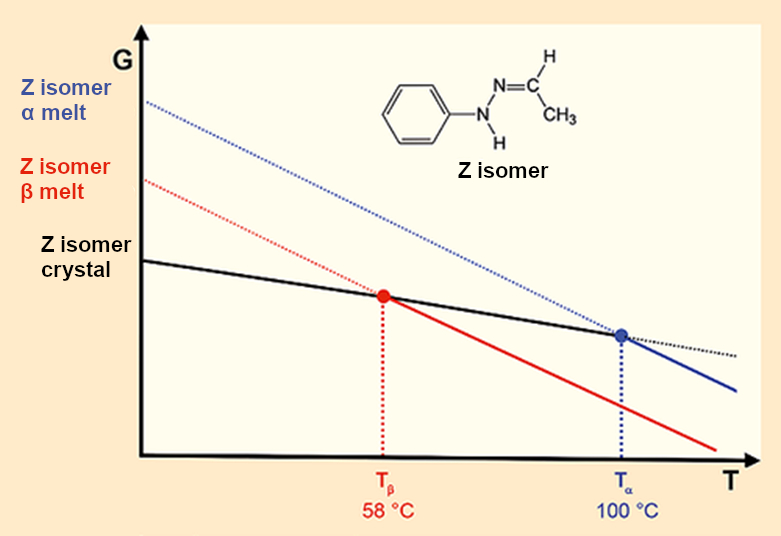
We do not want to be as one-sided as Fischer and throw thermodynamics overboard right away. Let us be open-minded and proceed with pragmatism. Let us assume that the α and β crystals do indeed exist and the laws of thermodynamics continue to apply. Perhaps we have not yet correctly applied them to Fischer’s hydrazone. Let us ask a seemingly simple question: When can a crystalline substance have two melting points? Manuel E. M. da Piedade at the University of Lisbon, Portugal, presents two acceptable possibilities [19]:

“There are either two different crystalline forms (polymorphism) or two different melts.”

Because the X-ray crystallographic data unambiguously prove that Fischer’s hydrazone crystallizes in only one lattice, we must warm to the thought that the two different melting points result from two different melts. A diagram depicting this idea can quickly be drawn up (see Fig. 7) but how can we picture this? How can a crystal melt two times, or sometimes in one way and at other times another way? Terry Threlfall is correct, if we believe in our experimental results, we shake up the thermodynamic order of the universe.

Figure 6. Fischer’s hydrazone: One crystal – one melting point – one melt.

Figure 7. Fischer’s hydrazone: Two crystals – two melting points – two melts.

8. A crystalline form can only melt at two temperatures if this results in two different melts.

2.2. In Search of the Two Melts

After looking at the crystals first, Hugo Meekes’ research group at Radboud University in Nijmegen, The Netherlands, changed the focus of their investigations, deciding to carry out a closer spectroscopic examination of the α and β melts. In an initial experiment, they obtained the ¹³C NMR spectrum of molten β crystals. To their great surprise, the β melt consists of two compounds, the Z- and E isomers of Fischer’s hydrazone (see Fig. 8).

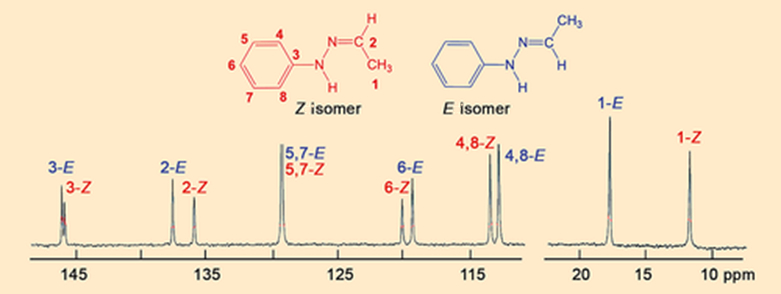Figure 8. ¹³C NMR spectrum of the β melt.

This ¹³C NMR spectrum forces a fundamental shift in our analysis, because we are suddenly dealing with two hydrazones and because a chemical reaction must have occurred for the Z isomer in the crystals to have been converted to the E isomer in the melt (see Fig. 9). We have to take both complications into account and broaden our view from one limited to thermodynamics to one encompassing chemical and kinetic components.

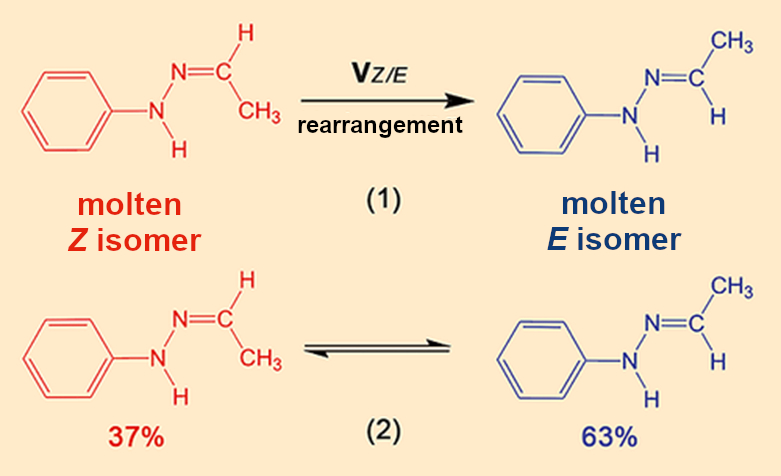Figure 9. Rearrangements between the two isomers.

9. Puzzle piece 4 is incorrect because the β melt is a mixture of the Z– and E isomers of Fischer’s hydrazone. This means that the chemical compositions of the crystal and the melt are different.
10. A chemical rearrangement reaction between the Z and E isomers occurs in the melt.

Hugo Meekes and Leyla Sö̌ütǒlu from Nijmegen went all out. They tracked the melting of the α and β crystals directly in the NMR spectrometer. The ¹H NMR spectra (see Fig. 10) prove that the Z/E rearrangement (see Fig. 9, Eq. 1) occurs so fast in freshly molten β crystals at 58 °C that the equilibrium (see Fig. 9, Eq. 2) is established instantly.

The larger proportion of the E isomer in the equilibrium shows that it is more thermodynamically stable than the Z isomer. This is why rearrangement (1) occurs spontaneously and the E/Z melt is more stable than the pure Z melt. The α crystals first liquify to a melt of primarily Z (see Fig. 10). At 100 °C, the Z/E rearrangement (1), which also begins immediately in this case, occurs so slowly that it takes almost an hour for the Z/E equilibrium (2) to be established.

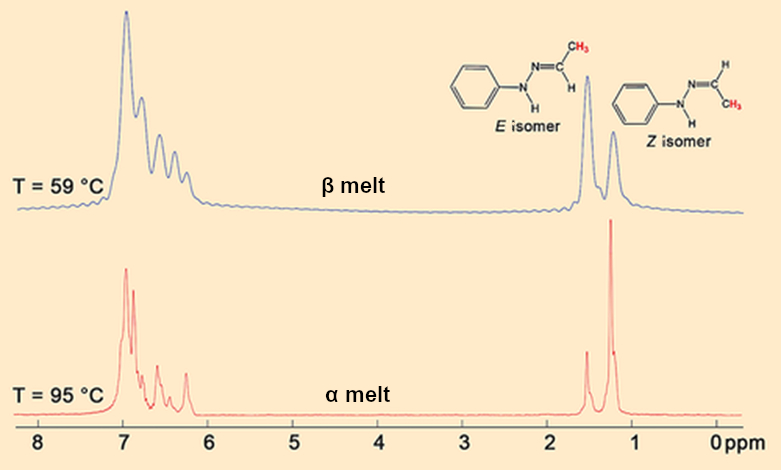Figure 10. ¹H NMR-spectra of fresh α and β melts.

11. Within the melt, the Z/E rearrangement occurs with a reaction rate of v_ZE (see Fig. 9, Eq. 1) until the lowest energy Z/E equilibrium (Eq. 2) is established.
12. In the β melt, v_ZE is high and equilibrium (2) is established instantly at 58 °C.
13. In the α melt, v_ZE is low, which means that the melt initially consists of only the Z isomer. The Z/E equilibrium (2) is established very slowly, even at 100 °C.

This NMR spectroscopic investigation delivered the last three pieces of the puzzle, which allows us to put together the whole picture (see Fig. 11). The unusual interplay of all of the factors brings to the fore the two melts required by thermodynamics: the α melt made of Z isomers and the β melt made of a Z/E mixture. Both melts originate in the different rates of Z/E rearrangement v_ZE, which is slow for the α melt and fast for the β melt.

Figure 11. Overview of the melting of Fischer’s hydrazone.

3. A Never-Ending Dilemma?

As nicely as the puzzle pieces assemble into the overall picture in Fig. 11, we cannot ignore the fact that this represents two separate melting diagrams: the upper one for the α crystalline form and the lower one for the β crystalline form. We cannot forget that all of the spectroscopic measurements and the X-ray crystal structure analysis unambiguously say that these two crystalline forms do not exist. We are still stuck in our dilemma, though our newly acquired knowledge of the details allows us to formulate it more precisely:

The α and β crystals are identical:
All spectroscopic measurements and the X-ray crystal structure analysis show no differences at all.
The α and β crystals are different:
The β crystals accelerate the Z/E rearrangement in their own melt; the α crystals do not do this.

Because there is no way out in sight, we are best off doubting both of these statements. On the one hand, it is clear that aside from IR and NMR spectroscopy, and X-ray crystal structure analysis, there are many other methods that have not yet been applied to Fischer’s hydrazone. Perhaps we have not chosen correctly.

On the other hand, we do not know which crystal property leads to the different rates of Z/E isomerization (see Eq. 1) in the melts. Let us ask ourselves how and, more importantly, by what the rate of reaction can be influenced. The reaction mechanism of the Z/E rearrangement is known (see Fig. 12). It is a rotation around the C=N double bond that is normally severely hindered and extremely slow. However, protons can speed up this reaction as catalysts because protonation of the nitrogen reduces the double bond character of the C=N double bond, making the rotation easier in the cation. Typical examples of this type of isomer are imines R¹R²C=N–R³ and related substance classes such as oximes (R³ = OH), semicarbazones (R³ = NH–CO–NH₂), hydrazones (R³ = NH₂), etc.

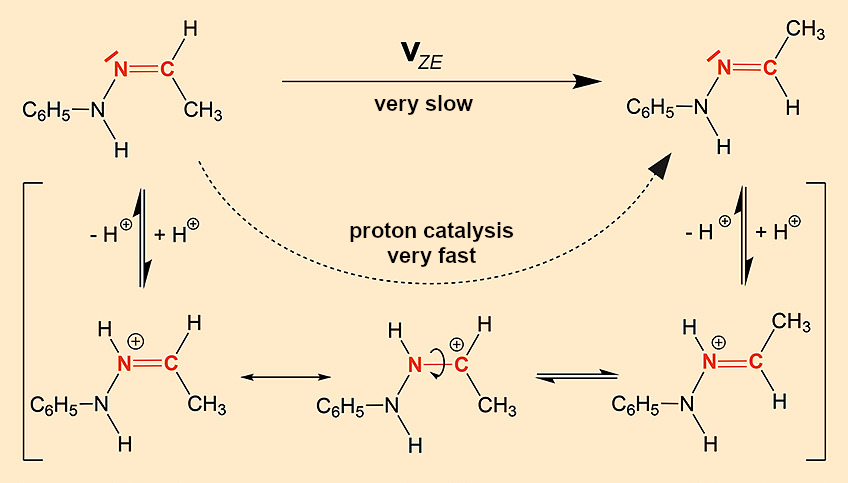Figure 12. Z/E isomerization of C=N double bonds.

With the word catalyst, it begins to dawn on us. The tiniest traces of acid on the surface of the crystal could act as catalysts. Both crystalline forms are obtained by crystallization from ethanol, α crystals after addition of bases and β crystals after addition of acids. It is no wonder that the β crystals, with their acid-tainted surfaces, so strongly accelerate the isomerization in their own melt.

It now becomes clear why Fischer’s drying of the hydrazone crystals in a desiccator over concentrated sulfuric acid was not a good idea. Even the hydrogen used by Lockemann and Liesche (see Part 1, Section 1.3 [11]) prevented oxidation but, having been passed through concentrated sulfuric acid, brought traces of sulfur dioxide into the desiccator, which left traces of acid on the surfaces of the crystals. The contradiction that the α and β crystals are either the same or different can, in the end, be solved with a Solomonic “neither nor”. It is correct that the α and β crystal interiors have identical structures, but they differ in the contamination of their surfaces with traces of acid.

Everything has fallen into place; everyone was right. We can excuse our transient doubt in the validity of thermodynamics because a devious catalytically driven red herring tricked us. Reassured, we can conclude that thermodynamics remains valid.

Indeed, Fischer’s hydrazone is absolutely unique among crystals, because this is the first case in which a confusing interplay between thermodynamics and kinetics determines a reaction rate and melting point. Even if Fischer’s hydrazone is an exotic outlier, it reminds us that the melting point is not only a property of the crystal, as many melting point tables lead us to believe. The melt also has a little something to say in the matter.

What do we call this surprising, singular phenomenon? Because it is not a simple melting point. Terry Threlfall has a decided opinion that does us some good and grounds us after so much confusion:

“If anyone wants to name it, they can do that. But if you ask me, scientific literature is already stuffed full of too many unnecessary terms.”

Acknowledgments

The author wishes to thank Dr. Hans Bauer, Berlin, Germany; Prof. Dr. Peter Luger and Dr. Sabine Streller, Free University of Berlin, Germany; Prof. Terry Threlfall, Southampton, UK, and Prof. Hugo Meekes, Radboud Universität Nijmegen, The Netherlands, for technical support in the introduction and for their critical and constructive review of the manuscript.